Турбулентность. Особенности турбулентного движения, Тензор турбулентных напряжений. Конвективные, адвективные и турбулентные потоки физических величин, страница 11

                          ,

где  - адиабатический градиент температуры. Поэтому первое слагаемое в скобках в выражении (15.12) равно

                                .

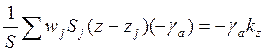Второе слагаемое также отлично от нуля из-за наличия ускорений, обусловленных выталкивающей силой. На  уровне z_j существует термическая составляющая ускорения: для более теплых частиц () ускорение положительно, для более холодных – отрицательно. Это значит, что частицы, прошедшие площадку на уровне z снизу (), были в среднем теплее окружающей среды и . Для частиц сверху – меньше нуля. В результате оказывается, что величина 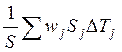 должна быть существенно положительной. Это означает, что в случае, когда средний градиент температуры равен адиабатическому (первые два члена в (15.12) компенсируют друг друга, остается третий положительный член), суммарный турбулентный поток тепла направлен вверх. Введем обозначение

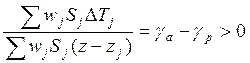                                  ,                                                              (15.13)

то есть,  . Обратите внимание, что в знаменателе дроби в (15.13) фактически фигурирует произведение .

Величина  называется равновесным градиентом температуры. С учетом (15.13) для плотности турбулентного потока тепла получаем

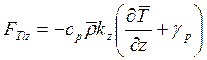                              .                                                                  (15.14)

Иными словами, когда градиент температуры воздуха равен равновесному, вертикальный турбулентный поток тепла равен нулю. Очевидно, этот равновесный градиент по величине должен быть меньше адиабатического градиента. Экспериментальные измерения показывают, что γ_р»(6 ±1) ^о/км, то есть, в пределах точности определения совпадает со средним вертикальным градиентом температуры в свободной атмосфере.

Здесь следует сказать несколько слов о зависимости коэффициента вертикального перемешивания от распределения температуры. При больших вертикальных градиентах температуры устойчивость атмосферы мала (наблюдаются большие вертикальные скорости движения и большие флуктуации скорости), и интенсивность турбулентного перемешивания растет (значения k_z велики). В противоположной ситуации, при инверсиях, коэффициент уменьшается в десятки и сотни раз.

В целом по земному шару суммарные турбулентные потоки тепла почти всюду направлены снизу вверх от поверхности Земли в атмосферу. Турбулентный перенос тепла является одним из механизмов передачи тепла от Земли атмосфере[15].

Горизонтальный  турбулентный перенос тепла

Согласно (15.12), общее выражение для плотности среднего турбулентного потока тепла вдоль оси x имеет вид

                   ,

                                          .

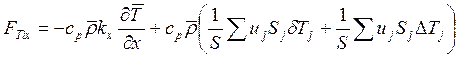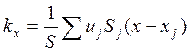Здесь последний член в выражении для плотности потока, очевидно, обращается в нуль, поскольку разность температур частицы и среды не приводит к возникновению горизонтальных ускорений. Следует отметить также, что составляющая скорости  здесь имеет смысл мгновенных пульсаций скорости вдоль оси x, поскольку речь идет о турбулентном потоке.

А вот первая сумма определенно не равна нулю, так как возможны сжатия и расширения воздушных частиц при их горизонтальных перемещениях, что будет приводить к изменению температуры. Если аккуратно учесть, что при адиабатических изменениях давления меняется и температура, то для плотности горизонтального турбулентного потока получим

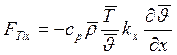                                    ,                                                                   (15.15)

где θ – потенциальная температура, то есть, температура, которую приобрел бы сухой воздух, если его адиабатически сжать до нормального давления. Мы приводим эту формулу без строгого доказательства, хотя существуют весьма простые доводы в пользу ее правильности. Действительно, выражение для теплосодержания единицы объема можно несколько модифицировать:

                                              ,

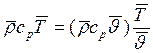где выражение в круглых скобках имеет смысл «потенциального теплосодержания» и не меняется при адиабатических сжатиях и расширениях. «Обычное теплосодержание» отличается от «потенциального» множителем  . Очевидно, что для плотности потока «потенциального тепла» справедливо выражение