Простейшие задачи динамики атмосферы

16. Простейшие задачи динамики атмосферы

16.1 Упрощение уравнений движения

Уравнения динамики атмосферы в том виде, в каком они получены в разд. 14,15, оказываются чрезвычайно сложными для практического использования. Однако в ряде случаев можно приближенно ввести значительные упрощения, исключая несущественные, малые по величине члены из уравнений. Эта процедура выполняется на основании оценок порядков величин отдельных членов в уравнениях, характерных для той или иной задачи. Обычно в ходе подобных оценок манипулируют различными безразмерными величинами, скомбинированными из характерных параметров рассматриваемого движения. Ниже показывается, как можно оценить влияние вращения планеты на движение, используя так называемое число Россби.

Число Россби [71]

Когда речь идет о крупномасштабных движениях атмосферы, подразумевается, что это движения, в значительной степени подверженные влиянию вращения планеты вокруг собственной оси. В качестве количественной характеристики степени важности вращения планеты при рассмотрении того или иного явления выступает число Россби, определяемое следующим образом.

Пусть L – характерный масштаб движения. В частности, если речь идет о движении циклонов или антициклонов, то в качестве такого масштаба естественно принять среднее расстояние между соседними циклоном и антициклоном. Обычно такое расстояние имеет величину порядка 1000 км. Заметьте, здесь речь идет именно о горизонтальном масштабе движения; для вертикальных масштабов в атмосфере будут совсем другие оценки. 

Соответственно, пусть U  будет характерной величиной скорости рассматриваемого движения. В нашем случае приемлемой оценкой является значение 20 м/с. Время, затрачиваемое на то, чтобы пройти выбранное расстояние с заданной скоростью определяется отношением L/U. Если это время много меньше периода вращения планеты вокруг своей оси, можно ожидать, что такой тип движения вряд ли окажется чувствительным к вращению за время реализации движения. Чтобы планетарное вращение существенно сказывалось на движении, должно быть обратное соотношение между временами:

                                       .

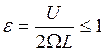Здесь Ω – угловая скорость вращения Земли (обратно пропорциональная периоду вращения), а безразмерный параметр ε называют числом Россби. Крупномасштабные течения в атмосфере (или океане), подверженные заметному влиянию вращения Земли характеризуются числами Россби порядка 1 или меньшими. В рассматриваемом случае с учетом угловой скорости вращения Земли Ω=7.3∙10^-5 с^-1 получаем ε=0.137. Следовательно, на перемещение циклонов и антициклонов вращение Земли оказывает существенное влияние. Далее мы уточним приведенные оценки. Обратите также внимание на то, что чем меньше характерная скорость движения, тем меньше характерные масштабы для движения, подверженного влиянию вращения Земли. Например, течение Гольфстрим характеризуется скоростью порядка 1 м/с, и, хотя характерный масштаб длины для него составляет 100 км, соответствующее число Россби равно 0.07. Поэтому такой тип течения естественно относить к типу крупномасштабных.

Одной из сил, определяющих состояние атмосферы, является сила тяжести. В случае крупномасштабных движений это наибольшая по величине сила, действующая в вертикальном направлении. Именно действие силы тяжести приводит к тому, что в большинстве случаев (для крупномасштабных движений – всегда) атмосфера оказывается динамически устойчивой по вертикали в том смысле, что масштаб движения воздуха в вертикальном направлении D  несоизмерим с горизонтальным масштабом: 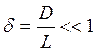. Результатом является то, что траектории крупномасштабного движения воздушных частиц выглядят очень плоскими.

Выше число Россби было введено, исходя из анализа кинематических особенностей движения. Однако эти особенности должны находить соответствующее отражение и в уравнении движения. Согласно последнему, относительное ускорение в сумме с ускорением Кориолиса равно сумме действующих на воздушную частицу  сил. Поэтому значение силы Кориолиса для рассматриваемого движения можно количественно оценить, сравнивая названные два вида ускорения. Порядок величины ускорения Кориолиса - 2ΩU. Порядок величины относительного ускорения – U²/L в предположении, что  имеет тот же порядок величины, что и . Отношение величины относительного ускорения к ускорению Кориолиса как раз и равняется числу Россби и для крупномасштабных движений должно быть мало:

                                 .

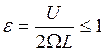Согласно полученному только что результату, в такой ситуации ускорение Кориолиса доминирует над ускорением относительного движения. Это вовсе не значит, что ускорение Кориолиса очень велико. Просто относительное ускорение в случае крупномасштабных движений оказывается несравнимо меньше ускорения Кориолиса.

В разд. 19 определен вектор абсолютного вихря

                        ,

где Ω – вектор угловой скорости вращения Земли, , V – вектор скорости относительного движения. Иными словами, абсолютный вихрь представляет собой сумму относительного и планетарного вихрей. Оценим соотношение между обоими. Нормальная к земной поверхности компонента планетарного вихря равна параметру Кориолиса:

                                 ,