Простейшие задачи динамики атмосферы, страница 7

Рассмотрим теперь установившееся равномерное движение воздуха с учетом турбулентного коэффициента перемешивания. При этом будем полагать последний постоянным в пределах пограничного слоя. Очевидно, это весьма грубое приближение. Однако оно вполне удовлетворительно передает основные черты воздушных течений в планетарном пограничном слое. При условии постоянства коэффициента турбулентной диффузии из системы уравнений (16.1) получаем

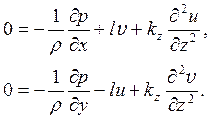                                                                   (16.6)

Далее, будем полагать, что горизонтальный градиент давления не меняется с высотой в пределах слоя достаточной толщины (это не «мешает» изменяться самому давлению с высотой). Тогда общее решение системы (16.6) можно записать в виде

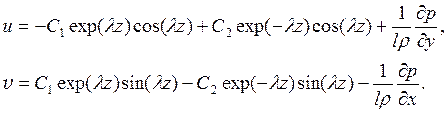
Здесь обозначено . Постоянные С₁, С₂  определяются из граничных условий. Первую следует положить равной нулю, поскольку скорость не может расти безгранично с высотой. Вторая определяется из условия равенства нулю скорости ветра у поверхности земли (z=0). Если ось y направлена по градиенту давления, тогда скорость геострофического  ветра равна 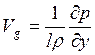, а для скоростей u и  получаем

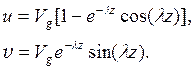
Отсюда для величины скорости находим                                     .

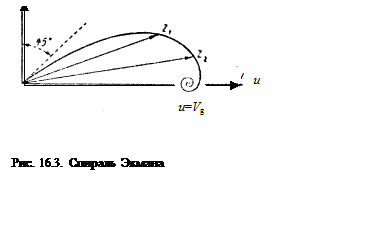Таким образом, скорость ветра постепенно увеличивается с высотой и на некоторой высоте достигает скорости градиентного ветра. Если изобразить вектор скорости в зависимости от высоты в координатах u, , получим логарифмическую спираль, называемую спиралью Экмана[4](рис. 16.3). Хотя коэффициент турбулентной вязкости полагался не зависящим от высоты (конечно, это не соответствует реальным условиям), полученный ход изменения направления и скорости ветра с высотой приближенно соответствует действительности.

Впервые достигнув на некоторой высоте  скорости геострофического ветра, ветер продолжает медленно расти,  достигает максимального значения и по направлению впервые совпадает с геострофическим. Высота H, на которой это происходит, определяется условием  =0. Получается . Далее, ветер продолжает медленно колебаться около направления геострофического ветра, а его скорость приближается к скорости геострофического ветра. Конечно, эти малые  колебания направления и скорости ветра не соответствуют реальности – они возникают из-за грубости нашей модели[5]. Однако в общих чертах модель качественно правильно передает изменчивость ветра с высотой в нижних слоях атмосферы.

Высота H определяет толщину слоя, в котором сказывается влияние земной поверхности на характере воздушных течений. Этот слой называется планетарным или пограничным  слоем или слоем Экмана. Его толщина, как видно, зависит от величины коэффициента турбулентного трения[6].

Ветер в приземном подслое

Нижние несколько десятков метров атмосферы образуют приземный подслой. Здесь наиболее сильно выражено влияние подстилающей поверхности, и здесь проявляется характерный и значительный ход таких  метеорологических элементов, как температура, влажность, ветер. Это же относится к вертикальным составляющим градиента названных элементов, резко отличающимся обычно от величин, соответствующих свободной атмосфере. Ниже мы конкретизируем определение приземного подслоя. Рассмотрим уравнение движения для однородного по горизонтали потока. Выбирая  направление оси x по направлению потока, получаем

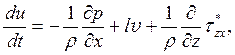
где последний член является проекцией силы трения, обусловленной молекулярной и турбулентной вязкостью, на горизонтальную ось x. Умножим это уравнение на плотность воздуха и проинтегрируем в слое от подстилающей поверхности до уровня z

                               .

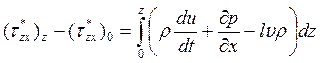Интеграл справа является непрерывной функцией верхнего предела, а составляющие разности слева на всех уровнях - величины, существенно отличные от нуля. Поэтому для не очень больших значений переменной zможно записать  

                                                        .