Неупорядоченное пульсационное движение можно, по крайней мере, качественно рассматривать как результат наложения турбулентных пульсаций различных масштабов. Здесь под масштабом движения подразумевается порядок величины расстояния, на котором существенно меняется пульсационная скорость. При развитии турбулентности сначала появляются крупномасштабные пульсации (соответствующий масштаб называют внешним масштабом турбулентности; пульсации такого масштаба содержат максимальный запас кинетической энергии), затем более мелкие. Другой подход к проблеме классификации пульсаций по размерам может быть построен на основе рассмотрения турбулентного движения как системы дробящихся вихрей: от первоначальных – крупных, ко все более мелким. Тогда характерными размерами пульсаций будут пространственные размеры вихрей, а характерными скоростями – скорости вихревого движения жидкости. В мелкомасштабных пульсациях заключена относительно малая часть всей кинетической энергии турбулентного движения.
В связи с
многомасштабностью развитой турбулентности можно ввести понятие чисел Рейнольдса
турбулентных пульсаций различных масштабов. Пусть ![]() -
линейный масштаб пульсации,
-
линейный масштаб пульсации, ![]() - порядок величины ее
скорости. Тогда соответствующее пульсации число Рейнольдса -
- порядок величины ее
скорости. Тогда соответствующее пульсации число Рейнольдса - ![]() . Чем меньше масштаб пульсации, тем меньше
соответствующее ему число Рейнольдса.
. Чем меньше масштаб пульсации, тем меньше
соответствующее ему число Рейнольдса.
При больших
числах Рейнольдса движения в целом велики также и числа Рейнольдса крупномасштабных
пульсаций. Но большие значения числа Рейнольдса эквивалентны малой вязкости. Отсюда
можно заключить, что для крупномасштабного турбулентного движения (основного в
турбулентном потоке) вязкость жидкости не играет существенной роли. Поэтому в
крупномасштабных пульсациях диссипация энергии мала. Она становится заметной
только для самых мелких пульсаций, которым соответствуют малые числа Рейнольдса
![]() . Именно в этих мелкомасштабных пульсациях,
несущественных с точки зрения общей картины движения жидкости, происходит диссипация
энергии ее движения за счет действия сил вязкости.
. Именно в этих мелкомасштабных пульсациях,
несущественных с точки зрения общей картины движения жидкости, происходит диссипация
энергии ее движения за счет действия сил вязкости.
Согласно
приведенным соображениям, энергия переходит от пульсаций самых больших масштабов
к пульсациям более мелких размеров практически без диссипации, и только на
уровне самых мелкомасштабных пульсаций энергия диссипирует и переходит в тепло.
Для поддержания этого процесса требуется наличие внешних источников энергии,
непрерывно передающих ее основному крупномасштабному движению. Основываясь на
таких соображениях, можно оценить порядок величины ![]() диссипируемой
энергии в единицу времени в единице массы жидкости. Поскольку крупномасштабные
пульсации не зависят от вязкости, то имеются всего 3 физические величины,
определяющие характер движения: плотность
диссипируемой
энергии в единицу времени в единице массы жидкости. Поскольку крупномасштабные
пульсации не зависят от вязкости, то имеются всего 3 физические величины,
определяющие характер движения: плотность ![]() , характерные
размеры потока
, характерные
размеры потока ![]() , и характерное изменение
средней скорости потока
, и характерное изменение
средней скорости потока ![]() на расстояниях порядка
на расстояниях порядка ![]() . Из них можно построить только одну
комбинацию нужной размерности, а именно
. Из них можно построить только одну
комбинацию нужной размерности, а именно
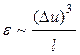 .
.
Из соображений размерности можно
также оценить характерный масштаб самых мелких пульсаций, где начинает играть
роль вязкость жидкости (так называемый внутренний масштаб турбулентности;
под действием вязкости кинетическая энергия таких пульсаций диссипирует,
превращаясь в тепло). Для этого следует составить комбинацию размерности длины
из определяющих величин: ![]() и
и ![]() . Результат имеет вид
. Результат имеет вид
![]() .
.
Надежных оценок внешнего масштаба турбулентности в атмосфере нет. Чаще всего в тропосфере и нижней стратосфере значения внешнего масштаба заключены в интервале 100-300 м на высотах 70 – 300 м и в интервале 1.5 – 2.5 км на бóльших высотах. В пределах приземного слоя атмосферы значение внешнего масштаба принимается равным высоте. Для вертикальных пульсаций внешний масштаб в 1.5 – 2 раза больше, чем для горизонтальных.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.