Ниже мы намерены рассмотреть несколько случаев движения воздуха, относящихся к движениям среднего масштаба. В такой ситуации возможно дополнительное упрощение в виде отказа от учета кривизны атмосферы. Понятно, что для крупномасштабных движений учет кривизны атмосферы обязателен. В приближении плоской атмосферы уравнения движения приобретают вид
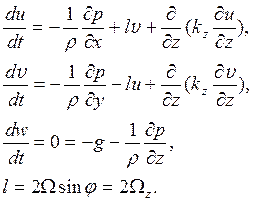 (16.1)
(16.1)
Здесь
дополнительно использовано то, что вертикальные ускорения и горизонтальные
градиенты скоростей обычно малы, и ими в первом приближении можно пренебречь. В
частности, в первом уравнении опущены члены 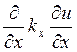 и
и 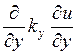 . Как следует из сказанного выше, в
свободной атмосфере можно отбросить члены, обусловленные силой трения, в
приземном слое – силой Кориолиса.
. Как следует из сказанного выше, в
свободной атмосфере можно отбросить члены, обусловленные силой трения, в
приземном слое – силой Кориолиса.
Для решения задач динамической метеорологии обычно пользуются не сферическими (с началом в центре Земли) и не обычными декартовыми горизонтальными координатами, а так называемыми «стандартными координатами» [17]. Последние получаются в результате приближенного перехода от точных сферических координат к декартовым. При этом учитываются следующие обстоятельства.
1. Толщина атмосферы мала по сравнению с радиусом Земли.
2. Если ввести характерные масштабы движения по горизонтали и вертикали, L, Z (имея в виду, что на этих расстояниях изменение скорости по порядку величины равно соответствующей составляющей скорости), можно заключить, что Z<<L. Справедливость неравенства нарушается лишь тогда, когда сам масштаб горизонтального движения мал, например, сравним с размерами кучевых облаков. Предполагаем также, что размеры горизонтальных движений малы по сравнению с радиусом Земли. Отсюда следует, что для атмосферных движений масштаба, малого по сравнению с радиусом Земли, вне полярных областей все квадратичные члены в уравнениях, порожденные сферической системой координат, могут быть отброшены в виду их малости.
3. Уравнение
движения для вертикальной компоненты скорости с большой точностью может быть
заменено уравнением статики – барометрической формулой - 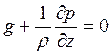 . Исключением являются движения мелкого
масштаба при больших скоростях, например, движения в случае смерча и,
по-видимому, движения внутри грозовых облаков.
. Исключением являются движения мелкого
масштаба при больших скоростях, например, движения в случае смерча и,
по-видимому, движения внутри грозовых облаков.
В результате оказывается, что для движений масштабов, малых по сравнению с радиусом Земли, с высокой точностью справедлива «стандартная» система координат, совпадающая с горизонтальной системой на каждой широте. Это приближение вполне адекватно при рассмотрении крупномасштабной динамики атмосферы в низких и средних широтах и неприменимо для высоких широт.
В свободной атмосфере влияние сил трения на атмосферные движения мало, и им можно пренебречь. Будем считать, что имеет место установившееся стационарное прямолинейное движение (сумма всех действующих сил равна нулю). Тогда из (16.1) имеем
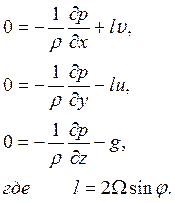
Первые два уравнения называются геострофическими. Они определяют движение, называемое геострофическим ветром[2]. Такое движение реализуется в случае уравновешивания отклоняющей силы Кориолиса силой барического градиента (градиента давления)[3].
Умножим
первое уравнение на u, второе - на ![]() и
сложим:
и
сложим:
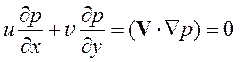 .
(16.2)
.
(16.2)
Таким образом, рассматриваемое движение происходит перпендикулярно направлению горизонтального градиента давления (здесь предполагается, что вертикальная составляющая скорости очень мала по сравнению со скоростью горизонтального движения и не дает вклада в скалярное произведение). Таким образом, геострофический ветер дует вдоль изобар. Из уравнений движения также следует
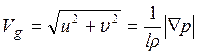 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.