Простейшие задачи динамики атмосферы, страница 11

Здесь сохранены  только самые важные члены, согласно  результатам  анализа  их  порядков  величин, и обозначено . Компоненты тензора напряжений  определены в разд. 15.1 и включают в себя молекулярные и турбулентные составляющие, причем последние играют определяющую роль. Тогда 

             .

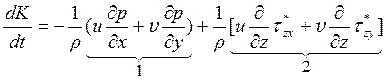Цифрой 1 обозначены члены, характеризующие изменение  кинетической  энергии  вследствие работы сил давления; цифрой 2  - изменение кинетической энергии за счет вязкости. Обратите внимание, что работа силы Кориолиса равна нулю, поскольку эта сила перпендикулярна скорости. Первый член описывает обратимый переход кинетической  энергии в работу сил давления и наоборот. Второй член – отвечает за необратимый процесс диссипации кинетической энергии. Рассмотрим роль этого члена в изменении кинетической энергии вертикального столба атмосферы единичного сечения (нужно умножить на dz  и проинтегрировать по всей высоте атмосферы):

                            .

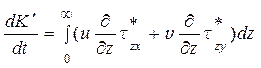Здесь штрих означает, что рассматривается только второй член предыдущего выражения. Интегрируем по частям:

                   .

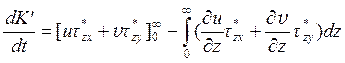Теперь воспользуемся аппроксимацией для компонент тензора турбулентных напряжений согласно 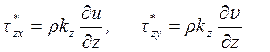   (см. разд. 15) и учтем, что на бесконечности =0,  потому что нет турбулентной вязкости из-за равенства нулю плотности воздуха. Поэтому

           .

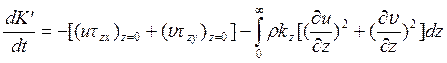Таким образом, под влиянием турбулентности происходит только потеря кинетической энергии. Первый  член  характеризует  потери  кинетической  энергии  за  счет  трения  о  нижележащие  слои  воздуха. Если  z=0  отвечает  поверхности  Земли, этот член  обращается  в  ноль  из-за  эффекта  прилипания  (скорость движения воздуха равна нулю). Второй член, очевидно, отрицателен и характеризует диссипацию  энергии  в  столбе  воздуха.

Если  воспользоваться  оценками  вертикального  распределения  ветра  в  нижней атмосфере  и  попытаться  рассчитать  этот  интеграл для приземного слоя атмосферы, то  получим D_пр~1 Вт/м². Для  остальной  части  нижней  атмосферы  D_ост~0,7 Вт/м². Это  потому, что в приземном  слое  очень  велики  вертикальные  градиенты  ветра.

В сумме  D~1,7 Вт/м². Приблизительно  такие  же  порядки  величин  существуют  в  области фронтальных  поверхностей  раздела  воздушных  масс (также  большие градиенты  скорости). Поэтому  суммарную  диссипацию  в  столбе  воздуха  можно  оценить  в  3 Вт/м². На нагрев  земной  поверхности  в  среднем  приходится  около  200 Вт/м²  солнечной  энергии. Оказывается, достаточно  превратить  1-2% этой энергии  в  кинетическую  энергию  движения  воздуха, чтобы  поддерживать   движение атмосферы.

Движения  воздушных  масс  происходят  из-за  неравномерности  нагрева  атмосферы  в  разных  участках. Движение  стремится  ликвидировать  эту  неравномерность, то есть, распределить  тепло  равномерно. Попутно  с  этим  процессом  часть  энергии  движения  расходуется  на  нагревание  воздуха вследствие трения. Тепло  порождает  движение, движение  превращается  в  тепло. Последнее  тепло  весьма  равномерно  распределяется  в  атмосфере  и  не  может  стать  источником  нового  движения. Более того, количество тепла, получаемое атмосферой в результате диссипации кинетической энергии за счет сил трения, очень мало по сравнению с теплом, получаемым за счет других источников. Именно это и послужило основанием возможности пренебречь такого рода  источником, когда рассматривалось первое начало термодинамики для атмосферного воздуха (разд. 13).

Интересные качественные результаты о процессе диссипации энергии в турбулентном течении можно получить, исходя из теории размерностей [36]. Турбулентное движение при больших числах Рейнольдса характеризуется нерегулярными беспорядочными пульсациями скорости в каждой точке потока. В условиях такой развитой турбулентности говорить о каком-либо упорядоченном движении можно только рассматривая средние характеристики движения, полученные посредством осреднения по достаточно большому промежутку времени или объему пространства. Будем называть отклонение мгновенного значения скорости от среднего значения  пульсационной скоростью.