Простейшие задачи динамики атмосферы, страница 8

Таким образом, горизонтальная  составляющая вектора напряжения суммарного трения в пределах достаточно тонкого приземного слоя атмосферы остается практически неизменной. Это суммарное напряжение является суммой молекулярного и турбулентного напряжений (см. разд. 15):

                                                      .

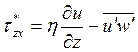В непосредственной близости к подстилающей поверхности вертикальные пульсации скорости невозможны, поэтому напряжение турбулентного трения равно нулю. Но уже на расстояниях порядка 1 мм турбулентное трение значительно превосходит молекулярное [17]. Поэтому, отвлекаясь от этого миллиметрового слоя, можно сказать, что величина и направление вектора напряжения турбулентного трения в приземном подслое не меняются с высотой. Анализируя аналогичным образом уравнение притока тепла, можно также определить толщину слоя, в пределах которого плотность вертикального турбулентного потока тепла постоянна и равна теплоотдаче подстилающей поверхности.

Аналогичный результат можно также получить, анализируя уравнение диффузии водяного пара: плотность вертикального турбулентного потока водяного пара в нижнем слое не зависит от высоты и равна скорости испарения с подстилающей поверхности.

Вообще говоря, толщины слоев, в пределах которых выполняется условие постоянства потоков названных величин (напряжение трения есть плотность вертикального потока количества движения), могут заметно различаться. Мы выбираем минимальную из толщин названных  слоев и называем ее толщиной приземного подслоя атмосферы.

Область применимости свойства постоянства потоков ограничена снизу уровнем порядка 1 мм над гладкой поверхностью, ниже которого нужного учитывать также и молекулярный обмен. Высота приземного подслоя обычно составляет несколько десятков метров.

В разд. 15 мы использовали концепцию Л. Прандтля и ввели путь смешения воздушной частицы, через который выразили коэффициент турбулентного обмена. Ниже мы воспользуемся понятием пути смешения для анализа профиля скорости горизонтального ветра в приземном подслое атмосферы.

В непосредственной близости к подстилающей поверхности путь смешения не может быть велик, поскольку перемещение турбулентных вихрей ограничивается близко расположенной твердой поверхностью. По мере удаления от подстилающей поверхности путь смешения должен увеличиваться, что в первом,  линейном приближении отражается соотношением

                                                        ,

где - постоянная Прандтля, значение которой экспериментально определено из аэродинамических измерений и составляет 0.38. Используя выражение для коэффициента турбулентного обмена через путь смешения (см. разд. 15), можно записать

                                              .

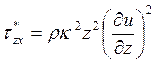Введем величину

                                           ,

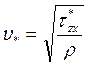называемую динамической скоростью. Очевидно, что в пределах приземного подслоя динамическая скорость – величина постоянная (о постоянстве напряжения суммарного трения уже говорилось выше, а плотность воздуха в тонком приземном слое также практически постоянна). Тогда из предыдущего соотношения получим[7]

                                            .

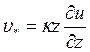Интегрируя, находим

                                           ,

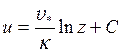где С – постоянная интегрирования. Отсюда следует, что профиль ветра в приземном подслое является логарифмическим. Это утверждение справедливо, когда стратификация слоя равновесная (безразличная), поскольку именно в этих условиях корректна использованная линейная связь между путем смешения и высотой.

Постоянную интегрирования можно выразить через так называемый уровень шероховатости z₀ – высоту, ниже которой средняя скорость обращается в ноль, и имеют место только турбулентные пульсации скорости[8]. Тогда

                                                   .

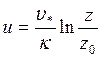Подобно проведенному выводу можно получить также и логарифмический закон изменения влажности воздуха с высотой в приземном подслое.