Простейшие задачи динамики атмосферы, страница 5

В слое трения  существует суточный ход скорости ветра. У земной поверхности над сушей максимум скорости ветра наблюдается около 14 часов местного времени, минимум ночью или утром. Начиная с приблизительно полукилометровой высоты, суточный ход получается обратным с максимумом ночью и минимумом днем. Причиной суточного хода скорости ветра является суточный ход интенсивности турбулентного обмена. Как показано ниже, толщина планетарного слоя обратно пропорциональна квадратному корню из коэффициента турбулентного обмена. При развитии конвекции в первую половину дня вертикальное перемешивание между приземным слоем атмосферы и вышележащими слоями усиливается, во второй половине дня и ночью - ослабевает. За счет притока воздуха сверху, имеющего большую скорость, скорость ветра у поверхности земли растет; за счет поднятия вверх воздуха из приземного слоя скорость ветра вверху уменьшается. При ослаблении турбулентного перемешивания ночью скорость ветра у поверхности земли падает, на высоте – растет. Над морем усиление конвекции приходится на ночное время, потому и суточный максимум ветра наблюдается ночью. Одновременно с суточным ходом скорости ветра по той же причине происходит и суточный ход изменения направления ветра.

 Градиентный  ветер– несколько  более  общее  понятие – обобщение  геострофического  ветра  на  случай  криволинейных  изобар. Такая  ситуация, в  частности, имеет  место  в  циклонах  и  антициклонах.

Напомним, что  геострофический  ветер – прямолинейное движение, когда сила  Кориолиса  уравновешивает  силу, обусловленную  постоянным градиентом  давления. Поскольку  сила  Кориолиса  в  северном  полушарии  действует  вправо  от  направления  движения, то  силы  давления  должны  действовать  в  противоположную  сторону, то есть, более  высокое  давление  должно  быть  справа. В случае циклона и антициклона движение воздуха осуществляется по кругу, а задача в целом обладает осевой симметрией, и градиент давления направлен по радиусу. Обозначим

 .

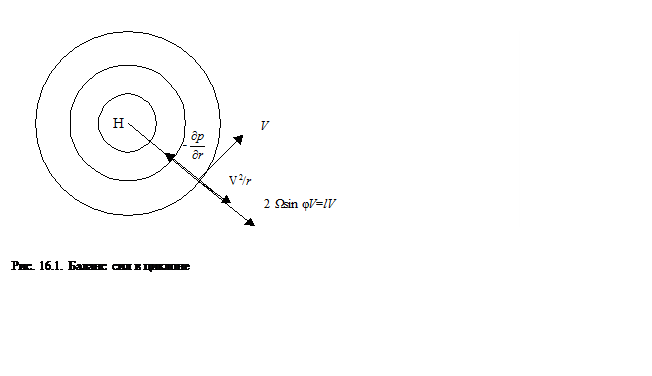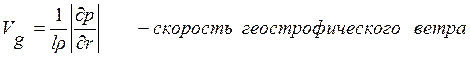Условие  баланса  сил в циклоне (см. рис. 16.1):

Здесь знак решения квадратного уравнения выбран так, чтобы  при  r→∞ (радиус кривизны стремится к бесконечности, следовательно, движение стремится к прямолинейному)     иметь естественно ожидаемый ответ:  V_ц→V_g.  Другое решение, как нетрудно убедиться, не удовлетворяет этому условию. Из найденного решения видно, что скорость ветра  в  центре  циклона равна нулю, а в других областях  меньше  скорости геострофического ветра (при том же значении градиента давления).

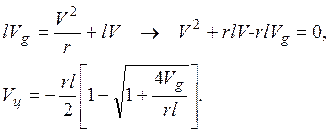
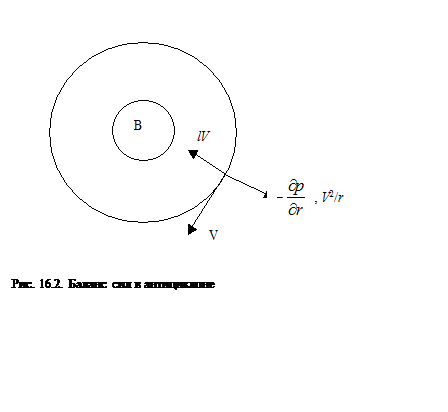В  антициклоне   ситуация  следующая (см. рис. 16.2):

                ,

.

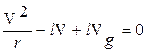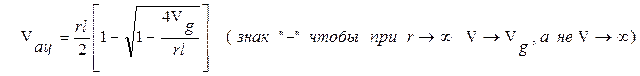В  центре  антициклона  скорость ветра  также равна нулю.  Однако  здесь  ограничен по величине  градиент  давления  :  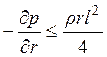(чтобы дискриминант квадратного уравнения не оказался отрицательным). Поэтому  скорость  ветра  в  центральной  части  антициклона  ограничена,  и  только  на  периферии  ветры  усиливаются, градиент  растет, изобары  сближаются. При  этом  V_ац >V_g . Явление  усиления ветра на периферии антициклона иногда  называют  струйным  течением  нижней  атмосферы.

Следует  помнить, что  рассмотренные  движения  воздуха (геострофический  и градиентный  ветры)  могут  соответствовать  реальности  только  на  высотах, превышающих  высоту пограничного  слоя (выше 1-1.5 км, где можно  пренебречь  вязким  и  турбулентным  трением; см. ниже). К  тому  же в реальных  условиях  изобары  имеют  весьма  сложные  очертания, а  влияние  нестационарности  движения  приводит  к  отклонению  траекторий  воздушных  частиц  от  изобар.

Мы  не  обнаружили  никаких  ограничений  для  скорости  ветра  в циклонах. Однако  в  реальных  условиях  градиенты  давления  и  скорости  ветра  в  циклонах  также  имеют  некоторые  предельные  значения (определяемые, скажем  так, энергетическими  возможностями  состояния  атмосферы).

16.3. Термический ветер