312Электронные измерительные системы
момент ti, но также значения сигнала в моменты времени, предшествующие ti, и значения, которые входной сигнал принимает в будущем. Поэтому такие схемы фильтрации реализуемы, как правило, только в форме цифрового алгоритма фильтрации в компьютере или в цифровом процессоре.
Мы уже видели, что ошибки
вследствие наложения спектров зависят от формы сигнала и вида его спектра.
Особенно важной при этом оказывается та часть спектра, которая сосредоточена
вблизи частоты ![]() / 2. Поскольку при проведении
измерений приходится иметь дело с сигналами различного типа, нереально найти
ошибки для каждого из этих (обычно не известных заранее) сигналов. Вот почему
для оценки точности системы сбора данных чаще всего в качестве тестового
сигнала выбирают шум.
/ 2. Поскольку при проведении
измерений приходится иметь дело с сигналами различного типа, нереально найти
ошибки для каждого из этих (обычно не известных заранее) сигналов. Вот почему
для оценки точности системы сбора данных чаще всего в качестве тестового
сигнала выбирают шум.
На вход системы подается
«белый шум» (то есть шум с не зависящей от частоты спектральной плотностью
мощности) с нормальным (гауссовым) распределением вероятностей по величине,
прошедший через так называемый «формирующий фильтр». Этот фильтр является
фильтром нижних частот, амплитудно-частотная характеристика которого остается
ровной до частоты среза ![]() и затем падает со
скоростью 6n дБ на октаву (то есть зависит от частоты как
и затем падает со
скоростью 6n дБ на октаву (то есть зависит от частоты как ![]() ). Шум на выходе такого фильтра n -го
порядка называют обычно «сигналом n-го порядка» с шириной спектра
). Шум на выходе такого фильтра n -го
порядка называют обычно «сигналом n-го порядка» с шириной спектра ![]() . Определяют среднеквадратическое значение
этого входного сигнала (стандартное отклонение гауссова распределения по
величине). Этот тестовый сигнал проходит через систему сбора данных с
фиксированной частотой взятия выборок и заданными характеристиками фильтра,
уменьшающего ошибки вследствие наложения спектров, и восстанавливающего
фильтра. Измеряется среднеквадратическое значение восстановленного сигнала. По
выполненным измерениям находят ошибку, вносимую системой сбора данных, и ее
зависимость от частоты взятия выборок, а также от типа и порядка примененных
фильтров. Эта ошибка является характеристикой, основанной, по существу, на
мощности сигнала, а не на максимальной мгновенной ошибке по
величине, как мы делали
. Определяют среднеквадратическое значение
этого входного сигнала (стандартное отклонение гауссова распределения по
величине). Этот тестовый сигнал проходит через систему сбора данных с
фиксированной частотой взятия выборок и заданными характеристиками фильтра,
уменьшающего ошибки вследствие наложения спектров, и восстанавливающего
фильтра. Измеряется среднеквадратическое значение восстановленного сигнала. По
выполненным измерениям находят ошибку, вносимую системой сбора данных, и ее
зависимость от частоты взятия выборок, а также от типа и порядка примененных
фильтров. Эта ошибка является характеристикой, основанной, по существу, на
мощности сигнала, а не на максимальной мгновенной ошибке по
величине, как мы делали
4.5 Системы сбора данных 313
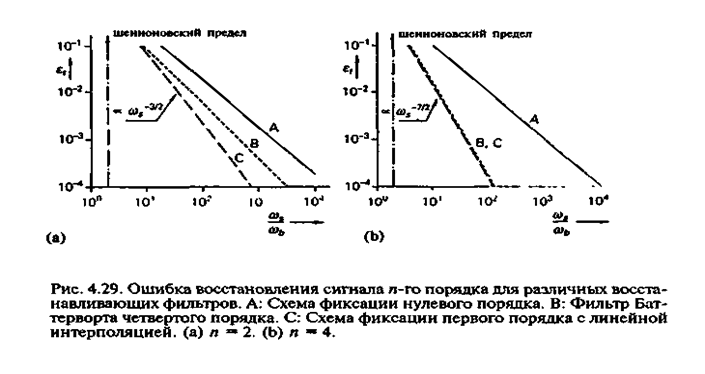
это для синусоидального сигнала. На рис. 4.29 представлены некоторые результаты для сигналов 2-го (n = 2) и 4-го (n = 4) порядков.
На этих графиках указана
зависимость относительной ошибки ![]() от отношения (
от отношения (![]() ) частоты взятия выборок
) частоты взятия выборок ![]() к ширине спектра
к ширине спектра ![]() (шумового)
сигнала на входе системы сбора данных. Здесь
(шумового)
сигнала на входе системы сбора данных. Здесь ![]() —
полная ошибка в среднеквадратическом значении восстановленного тестового
сигнала. На графике приведена ошибка, вносимая только при восстановлении в предположении,
что фильтр, уменьшающий ошибки вследствие наложения спектров, отсутствует.
Вычисляя мощность части тестового сигнала, спектр которой расположен в области
высоких частот, можно получить следующее выражение для ошибки при достаточно
крутом спаде частотной характеристики восстанавливающего фильтра:
—
полная ошибка в среднеквадратическом значении восстановленного тестового
сигнала. На графике приведена ошибка, вносимая только при восстановлении в предположении,
что фильтр, уменьшающий ошибки вследствие наложения спектров, отсутствует.
Вычисляя мощность части тестового сигнала, спектр которой расположен в области
высоких частот, можно получить следующее выражение для ошибки при достаточно
крутом спаде частотной характеристики восстанавливающего фильтра:
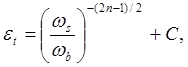
где n — порядок сигнала, а С — произвольная постоянная.
Из нашего предыдущего
рассмотрения нам известно, что ошибки восстановления могут приводить к большим
ошибкам, вносимым системой сбора данных в целом. Давайте теперь примем во
внимание другой источник ошибок, каким является процедура уменьшения ошибок
вследствие наложения спектров. Поскольку мы вольны выбирать граничную частоту
восстанавливающего фильтра (как это имеет место в случае аналоговых фильтров),
мы можем оптимизировать систему сбора данных в отношении полной ошибки ![]() . На рис. 4.30 показан результат такой
оптимизации, достигаемой за счет баланса между ошибками исключения и ошибками
включения. В этом частном примере
. На рис. 4.30 показан результат такой
оптимизации, достигаемой за счет баланса между ошибками исключения и ошибками
включения. В этом частном примере ![]() , а граничная частота
восстанавливающего фильтра
, а граничная частота
восстанавливающего фильтра ![]() изменяется от 0,1
изменяется от 0,1![]() до 10
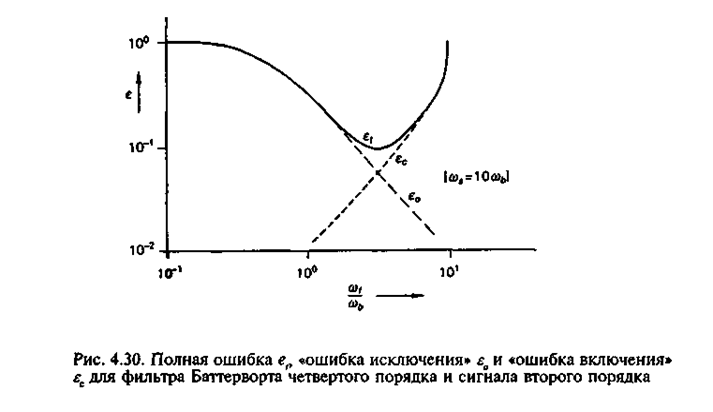
до 10![]() . На рис. 4.30 представлен случай, когда в качестве восстанавливающего
. На рис. 4.30 представлен случай, когда в качестве восстанавливающего
314 Электронные измерительные системы
применен фильтр Баттерворта
четвертого порядка, а тестовый сигнал второго порядка имеет ширину спектра ![]() .
.
Полная ошибка ![]() состоит из ошибки исключения
состоит из ошибки исключения ![]() и ошибки включения
и ошибки включения ![]() , поэтому
, поэтому
![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.