Электронные измерительные системы. Цифровые вольтметры. Осциллографы. Системы сбора данных, страница 11

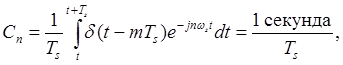
где m выбрано таким образом, чтобы . Поскольку

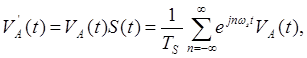
преобразование Фурье для  имеет вид:

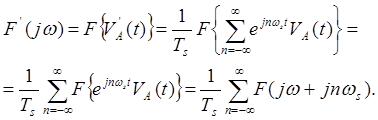
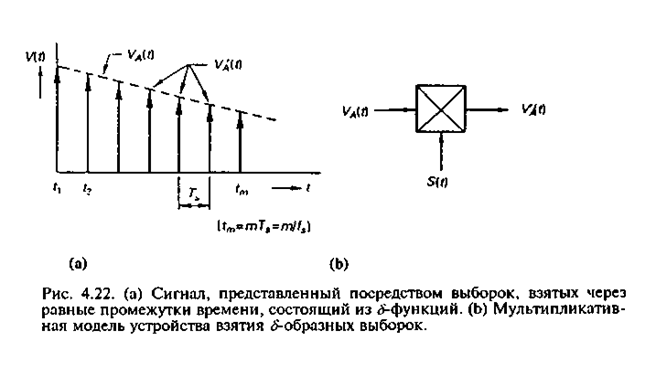
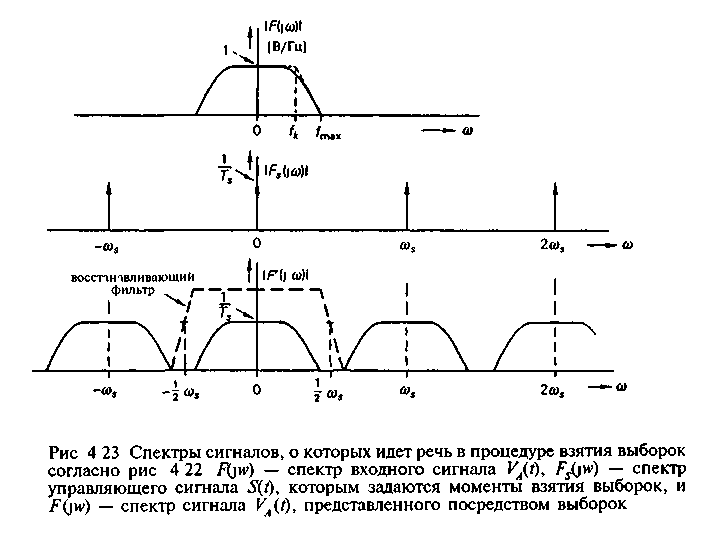
Здесь F(jw) — преобразование Фурье от входного сигнала V_A(t). Значе­ния |F(jw)| идентичны амплитудному спектру входного сигнала V_A(t), выра­женному в В/Гц. Из нашего вывода следует, что амплитудный спектр сигна­ла, представленного посредством выборок, F(jw) равен спектру входного сигнала F(jw), умноженному на 1 / Т_S и повторенному симметрично по обе стороны от каждой из частот nw_s. Таким образом, как видно из рис. 4.23, спектр сигнала, представленного посредством выборок, является совокуп­ностью бесконечного числа копий низкочастотного спектра входного сиг­нала F(jw), располагающихся симметрично относительно частот nw_s, кото­рые, в свою очередь, являются гармониками частоты, с которой берутся выборки w_s. Любая одна такая копия содержит всю информацию о входном сигнале. Говорят, что при таком повторении спектров происходит их «нало­жение». Нулевая копия лежит в полосе частот, занимаемой спектром исход­ного сигнала , а n-я копия — в окрестности частоты nw_s.

Подобное повторение копий спектра происходит также и в том случае, когда процедура взятия выборок не является столь идеальной. Например, при ненулевой длительности импульса, посредством которого осуществля­ется взятие выборки, и даже в том случае, когда выборочное значение удер­живается схемой выборки и хранения в течение всего периода взятия выбо­рок T_s, происходит указанное повторение копий спектра. Правда, копии с большими номерами являются при этом меньшими по величине, нежели в рассмотренном случае взятия выборок с помощью d-функций.

Из рис. 4.23 видно, что пока наибольшая частота входного сигнала f_max остается меньше половины частоты f_s, с которой берутся выборки, мы имеем возможность восстановить из спектра F(jw) спектр     исходного    сигнала       (выбрать нулевую  

копию) с помощью фильтра нижних частот. Такой фильтр устраняет все копии, находящиеся на оси частот вне его полосы пропуска­ния. Такие фильтры называют «восстанавливающими» или «интерполирую­щими» фильтрами. Если бы частота f_max была очень близка к значению f_S / 2, то нам понадобился бы фильтр нижних частот с очень крутым спадом час­тотной характеристики (с прямоугольной характеристикой) . Нельзя постро­ить фильтр с такой характеристикой для работы в «реальном времени». Прав­да, мы могли бы записать сигнал, и позднее, когда весь сигнал известен полностью, с помощью математических манипуляций восстановить исход­ный сигнал. Мы создали бы таким образом фильтр, не удовлетворяющий «принципу причинности», это такой фильтр, в котором используется зна­ние об изменениях входного сигнала в будущем. Поэтому практический вы­вод таков: пока , мы в состоянии безошибочно восстановить вход­ной сигнал

Ситуация становится совсем другой, когда упомянутое условие не вы­полняется, как это показано на рис. 4.24. Мы видим, что в этом случае копии спектров начинают накладываться друг на друга. При этом уже нет возмож­ности безошибочно восстановить нулевую копию даже при наличии идеаль­ного фильтра нижних частот.

На рис 4 24(b) показано, как выглядит в этом случае результат во вре­менной области.  Выборки берутся из синусоидального входного сигнала V_A(t) с частотой .   Пытаясь восстановить исходный сигнал, мы пропускаем  выборки через фильтр нижних частот с частотой среза /2. В результате получаем