Электронные измерительные системы. Цифровые вольтметры. Осциллографы. Системы сбора данных, страница 10

величины сигнала. Кроме того, входной сигнал в небольшой степени будет продолжать влиять на выходное напряжение в течение интервала вре­мени, когда схема находится в режиме хранения. Это явление называют «сквозным прохождением» входного сигнала.

Поскольку апертурное время обычно мало, максимальная скорость взя­тия выборок определяется временем захвата и временем преобразования в АЦП. Апертурным временем обусловлена задержка момента взятия выбор­ки, при этом вносится временная ошибка. Из-за апертурной погрешности имеет место неопределенность в моменте фактического взятия выборки. Го­ворят, что происходит дрожание. От погрешности в коэффициенте передачи зависит, насколько большой будет ошибка в значении выборки  (при постоянном входном сигнале, когда апертурное время не вносит ошибки). При очень больших отрезках времени, в течение которых схема находится в режиме хранения, мы сталкиваемся с необходимостью учитывать ошибки, обусловленные зависимостью величины сигнала от времени из-за спада на­пряжения на запоминающем конденсаторе.

Теперь мы обратимся к теории, лежащей в основе представления сигна­лов посредством выборок. На временных диаграммах на рис. 4.20 моменты взятия выборок расположены на оси времени не равномерно. Поэтому в дальнейшем мы не сможем восстановить форму входного сигнала. В ряде приложений моменты взятия выборок устанавливаются на оси времени слу­чайно. При таком случайном взятии выборок информация о форме теряется. По случайным выборкам мы можем определить только плотность распреде­ления вероятностей. Таким образом, случайные выборки дают нам статис­тическую информацию о величине входного сигнала. Это означает, что та­ким способом мы можем измерить среднеквадратическое и пиковое значе­ния входного сигнала, определить диапазон принимаемых им значений и т.п., но только не форму сигнала или его спектр.

Во многих случаях взятие выборок сигнала осуществляется в равноотсто­ящие моменты времени. Тогда важно решить вопрос о том, как много выбо­рок необходимо брать в единицу времени, чтобы иметь возможность доста­точно полно описать непрерывный по времени сигнал. Производя взятие выборок, мы не хотим потерять информацию, однако мы не хотим также брать выборки слишком часто. Ответ на этот вопрос дает теорема Шеннона о выборках. В этой теореме утверждается, что для восстановления (без оши­бок) исходного сигнала по его выборочным значениям, взятым через рав­ные промежутки времени, частота взятия выборок f_S должна более, чем вдвое, превосходить частоту f_max самой высокочастотной составляющей, имеющей­ся в непрерывном входном сигнале. Необходимо отметить, что под «вход­ным сигналом» здесь понимается не самый сигнал, являющийся предметом рассмотрения, а сигнал, включающий также все компоненты искажений и шума. Таким образом, в теореме предполагается, что существует такая мак­симальная частота f_max, выше которой спектральная плотность мощности равна нулю.

Чтобы представить себе, что произойдет, если это требование не будет выполнено, рассмотрим частотный спектр, возникающий в результате взя­тия выборок непрерывного по времени сигнала. Ради простоты, речь пойдет

только о значениях сигнала, представленного посредством выборок, в мо­менты взятия выборок (см. рис. 4.22).

Сигнал, представленный посредством выборок, можно записать как про­изведение аналогового входного сигнала V_A(t) и сигнала S(t), представляю­щего собой последовательность равноотстоящих единичных d-импульсов d(t – mТ_S). Таким образом, имеем:

где

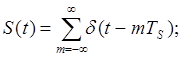
d-функции d(t – mT_s) называют также импульсами Дирака. Это функции, которые не равны нулю только в точке t = mT_s, и такие, что площадь под ними, получаемая в результате интегрирования по времени, равна единице (одной секунде). Поскольку сигнал S(t) является периодическим, его мож­но представить в виде ряда Фурье:

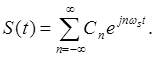
Коэффициенты Фурье С_n равны:

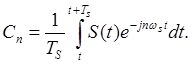
Поскольку значения S(t) (на интервале (t, t + Т_S)) не равны нулю только в точках mT_s справедливо следующее равенство: