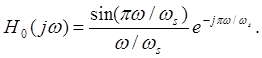
Здесь ![]() — частота взятия выборок. Чтобы получить
передаточную функцию такого фильтра с фиксацией нулевого порядка, можно
воспользоваться схемой, представленной на рис 4.26, предположив, что
блок S представляет собой
— частота взятия выборок. Чтобы получить
передаточную функцию такого фильтра с фиксацией нулевого порядка, можно
воспользоваться схемой, представленной на рис 4.26, предположив, что
блок S представляет собой
4.5 Системы сбора данных 309
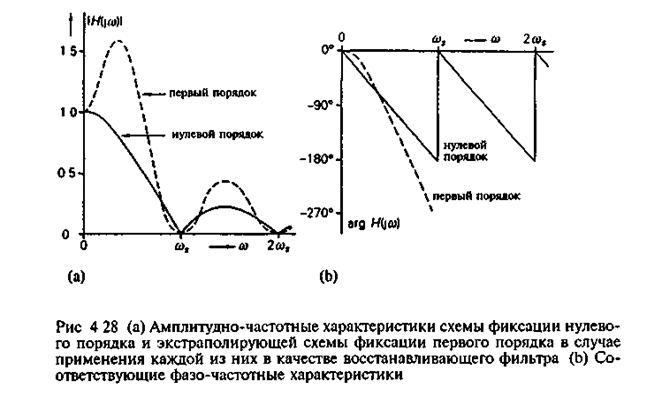
идеальное устройство взятия выборок с использованием d-функций, а блок R является схемой фиксации нулевого порядка. На рис. 4.28 приведена частотная характеристика этого восстанавливающего фильтра. Мы видим, что этот фильтр не вносит фазовых искажений; сдвиг фаз изменяется с частотой линейно.
Найдем максимальную мгновенную ошибку, возникающую на выходе такой схемы, для синусоидального сигнала V(t) = A sin(wt). Ошибка будет максимальной в точках пересечения нуля. В этом месте скорость изменения сигнала равна dV(t)/dt = Аw. Но она равна также максимальной ошибке DV, деленной на период Ts, с которым берутся выборки. Следовательно, можно считать, что DV= AwTs. Тогда максимальная относительная ошибка по величине равна:
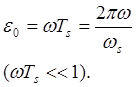
Таким образом, применяя
для восстановления аналогового сигнала схему фиксации нулевого порядка,
необходимо брать, по крайней мере, 628 выборок на периоде синусоидального
колебания, чтобы максимальная ошибка по величине была меньше 1%. Однако мы уже
знаем, что теоретически для безошибочного восстановления достаточно, чтобы
частота взятия выборок удовлетворяла неравенству: ![]() . Столь
большое расхождение тесно связано с тем, что схему фиксации нулевого порядка
легко реализовать, но в качестве фильтра она не обеспечивает при этом
эффективного восстановления.
. Столь
большое расхождение тесно связано с тем, что схему фиксации нулевого порядка
легко реализовать, но в качестве фильтра она не обеспечивает при этом
эффективного восстановления.
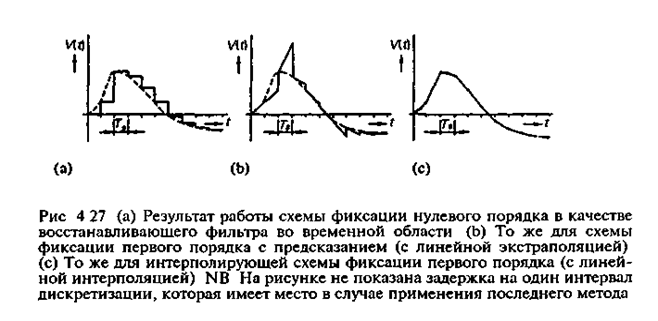
На рис. 4.27(b) приведена временная диаграмма для так называемой «схемы фиксации первого порядка с предсказанием». В этой схеме берутся значения входного сигнала в точках отсчета и по последнему интервалу между соседними выборками производится экстраполяция скорости изменения сигнала.
310 Электронные измерительные системы
Поэтому данную схему называют также «устройством, осуществляющим линейную экстраполяцию». Если такое устройство с линейной экстраполяцией используется в качестве восстанавливающего фильтра, то его передаточная функция имеет вид:
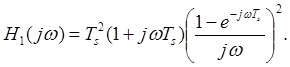
Эта передаточная функция также представлена на рис. 4.28. Нетрудно видеть, что при таком методе восстановления фактически происходит усиление высокочастотных составляющих и не обеспечивается линейность фазо-частотной характеристики. Большой сдвиг фаз на высоких частотах у восстанавливающих фильтров этого типа приводит к тому, что системы сбора данных, в которых такой фильтр является одним из узлов в петле обратной связи, особенно склонны к самовозбуждению. При таком поведении передаточной функции на высоких частотах устойчивость в области нижних частот перестает быть решающим фактором. Производя необходимые вычисления, можно получить следующее выражение для максимальной мгновенной ошибки по величине в случае синусоидального сигнала:
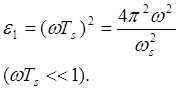
В схемах фиксации первого порядка (а также в схемах более высокого порядка) ошибка максимальна вблизи пиковых значений синусоидального сигнала. Для получения 1%-ной ошибки нам нужно примерно 63 выборки на период (при синусоидальном сигнале).
На рис. 4.27(с) приведена временная диаграмма, характерная для восстанавливающих схем другого типа, а именно — для линейно интерполирующих схем фиксации первого порядка. В такой схеме осуществляется линейная интерполяция между соседними выборками, и в моменты отсчета сигнал на выходе схемы совпадает с выборочным значением входного сигнала. Это возможно, естественно, только в том случае, когда известны оба граничных значения на концах интервала интерполяции. Поэтому на выходе интерполирующей восстанавливающей схемы сигнал появляется с задержкой по отношению ко входному сигналу, по меньшей мере, на один период, с которым берутся выборки Можно показать, что при синусоидальном сигнале максимальная мгновенная ошибка по величине для восстанавливающего фильтра с линейной интерполяцией равна:
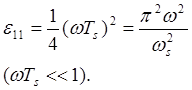
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.