Алгоритмы первичной обработки информации в АСУТП, страница 8

При программной реализации фильтра скользящего средне­го расчет сглаженного значения уф(]) в очередном /-том цикле проводится по формуле

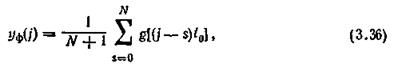
где N—T$,lto— параметр настройки фильтра

Для расчета по формуле (3.36) требуется хранить в памяти УВМ (N+1) значение функции g(jt₀).

Статистические фильтры. Статистическими называют фильтры, которые в аналоговом варианте представляют собой параллель­ное соединение (n+1) цепочек, состоящих из усилительного зве-

на и звена чистого запаздывания. Передаточная функция такого фильтра

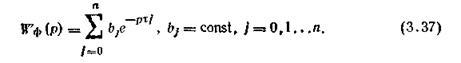
Статистический фильтр нулевого порядка. Это простейший среди фильтров данной группы. Его передаточная функция по­лучается из формулы (3.37) при N=0, т. е. это просто усили­тельное звено, выходной сигнал которого

При непосредственном использовании формулы (3.38) сглажен­ная функция у₀(0 будет являться смещенной оценкой полезного сигнала y(t), т. е. ее математическое ожидание не будет равно m_g. Действительно, усредняя левую и правую части (3 38) с уче­том (3.3) и m_е=0, получим:

Для получения несмещенной оценки к правой части (3 38) необ­ходимо прибавить постоянный член а, удовлетворяющий условию

откуда

Таким образом, формула (4 38) приобретает вид

Оптимальное значение параметра настройки b₀, полученное из необходимого условий минимума функции Dф (bo), равно

Ему соответствует минимальная    среднеквадратичная  погреш­ность фильтрации:

Как видно из (3.42), статистический фильтр нулевого порядка

при  оптимальной   настройке   снижает  случайную  погрешность сигнала измерительной информации в (1+k) раз

При программной реализации статистического фильтра ну­левого порядка расчет сглаженных значений производится по формуле:

Статистический фильтр первого порядка. Его передаточную функцию получают из (3.37) при N=1:

где bо, b1, т — константы.

Во временной области уравнение этого фильтра имеет сле­дующий вид:

Усредняя левую и правую части этого выражения и учиты­вая (3.3), получим: M[y^(l)}=(b₀+1)ni_tt.

Для выполнения условия несмещенности оценки уф((), т. е. условия М[yф(t)] = my, коэффициенты b₀и b1, очевидно, должны удовлетворять соотношению b1=1-b0,, с учетом которого форму­ла (3.43) приводится к виду:

где bо и т — параметры настройки статистического фильтра первого порядка.

Погрешность    фильтрации е_ф((),    согласно    (3.3),  (3.21) и (3.44), равна

а дисперсия погрешности

Оптимальное значение параметра настройки b₀получаем из ус­ловия

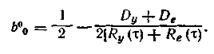
В большинстве случаев статистические фильтры реализуют­ся программно, поэтому второй параметр настройки т совпадает с периодом tо квантования по времени функции g(t).

Сравнительный анализ фильтров по совокупности показате­лей (точности, трудоемкости, потребному объему памяти УВМ и др.) показал [24], что для аналогового варианта целесообраз­но использовать экспоненциальный фильтр, а для программной реализации — экспоненциальный или статистический фильтр первого порядка.

3.4. АНАЛИТИЧЕСКАЯ ГРАДУИРОВКА ИЗМЕРИТЕЛЬНЫХ ПРЕОБРАЗОВАТЕЛЕЙ  И  КОРРЕКЦИЯ   РЕЗУЛЬТАТОВ  ИЗМЕРЕНИИ

В метрологии градуировкой называют операцию, с помощью которой делениям шкалы измерительного прибора придают оп­ределенные численные значения, выраженные в единицах изме­рения определяемой величины [27] Аналогичный смысл вкла-дывают в понятие аналитической градуировки ИП: это опера­ция определения (восстановления) значения х измеряемой вели­чины по сигналу у измерительной информации на выходе ИП (см рис. 31). Операцию аналитической градуировки выполняют с использованием градуировочной характеристики ИП, пред­ставляющей собой функцию, обратную его номинальной статиче­ской характеристике (3.2):

где  x^г — значение  измеряемой   величины,  соответствующее   по   градуировоч-ной характеристике  ИП  значению у  сигнала  измерительной  информации