Другие предметы \ Теория автоматического управления

Алгоритмы первичной обработки информации в АСУТП, страница 4

где М — знак математического ожидания.

Дисперсия погрешности экстраполяции равна:

где rk(v)—автокорреляционная функция случайного процесса g(t)

Из формулы (3.14) следует, что дисперсия погрешности экстраполяции зависит от т и достигает наибольшего значения при т—*t_Q. Усредняя А? (т) по т в пределах от 0 до /₀, окончательно получим:

где R_K(i)—аитокорриляционная функция случайного процесса g(t)

(3.15)

Это выражение позволяет рассчитать дисперсию погрешности экстраполяции по заданному периоду квантования t₀ и автокорреляционной функции R_g. Его же можно использовать для определения периода квантования t , если задано наибольшее допустимое значение среднеквадратичной погрешности экстраполяции ве* и известна автокорреляционная функция R_g(τ). Для этого удобно использовать графоаналитический метод (рис. 3.6).

По графику функции Rg(τ) определяют такое значение τ= t₀ при котором удвоенная средняя высота заштрихованной фигуры ABC(т. е. удвоенный отрезок ДЕ) будет равна заданному значению (σ_e*)² = D_e. Если ИИК содержит звено чистого запаздывания to (например, ввиду необходимости транспортиро-

Рис. 3.6. К расчету среднеквадратичной погрешности экстраполяции

Рис. 3.7. Линейная интерполяция функции g(l)

вания пробы от технологического потока до чувствительного элемента ИП), то для расчета среднеквадратичной погрешности экстраполяции можно использовать формулу (3.15) с заменой в ней пределов интегрирования: нижнего на т₀, а верхнего — на

t₀ +τ₀

Наряду с ИП непрерывного действия в АСУТП применяют и датчики дискретного действия, например хроматографы. Они осуществляют квантование по времени измеряемой величины с собственным периодом t_g, который обычно значительно выше периода опроса t₀. В этом случае результирующий период квантования по времени в данном ИИК определяется из условия

Для оценки погрешности экстраполяции можно использовать выражение (3.15) с заменой в нем t₀на t_g.

Линейная интерполяция (рис. 3.7) является простейшим методом интерполяции, в основе которого лежит кусочно-линейная аппроксимация функции g(t) на интервале значений

Уравнение прямой, проходящей через точки g(jt₀) и g((j+1)t₀ )можно записать в виде:

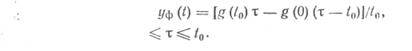
Погрешность линейной интерполяции

Подставляя в это выражение значение уф(1) из формулы (3.16), возводя его в квадрат и усредняя по множеству интервалов, а затем по т в пределах от 0 до /₀, получаем выражение для дисперсии погрешности линейной интерполяции:

В литературе описаны и другие, более сложные методы ин-

терполяции и экстраполяции [24], однако на практике их при-

меняют редко. Современные УВМ обеспечивают достаточно вы-

сокую частоту опроса ИИК, поэтому обычно удается обеспе-

чить требуемую точность восстановления измеряемых величин,

используя простейший метод ступенчатой экстраполяции. Обыч-

но среди десятков и даже сотен ИИК можно выделить несколь-

ко групп параметров, близких по частотным спектрам. Тогда

можно выбрать общий период опроса для каждой группы дат-

чиков. Например, в производстве разбавленной азотной кислоты

опрос группы датчиков, контролирующих малоинерционный про-

цесс контактного окисления аммиака, проводится с периодом

15 с, а опрос датчиков на инерционном процессе абсорбции —

с периодом 2 мин.

Выбор частоты опроса измерительных преобразователей через число нулей случайного процесса. Выбор частоты опроса t₀ по формуле (3.15) требует знания корреляционной функции R_g(i) случайного процесса g(t). Для получения оценки корреляционной функции необходим значительный объем вычислений. Кроме того, часто проще и естественнее задать не дисперсию ошибки D_eот замены непрерывного случайного процесса ступенчатым, а отношение этой величины к дисперсии случайного процесса D. Учтем также важность гарантии того, что выбранная частота опроса не приведет к появлению большей относительной погрешности, чем заданное значение, т. е. важно получить оценку сверху для периода опроса t₀ ,

1 2 3 4 5 6 7 8 9 10 11 12 13 14

Скачать файл