Другие предметы \ Теория автоматического управления

Алгоритмы первичной обработки информации в АСУТП, страница 2

Следующим видом преобразования, которому подвергается сигнал измерительной информации в ИИК, является квантова­ние по уровню, выполняемое аналого-цифровым преобразовате­лем (АЦП). При этом амплитуды импульсов g(jt0) преобразу­ются в числа g*(jt0), выраженные в коде, с которыми в даль­нейшем оперирует ЦВМ. Современные управляющие вычисли­тельные машины, как правило, используют двоичный код и опе­рируют с числами, имеющими 8 или 16 разрядов. Операция квантования дискретной величины g(jt0) по уровню описывается следующим выражением:

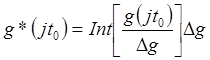                                                   (3.4)

где Int(r) — функция «целая часть от r»;  — шаг квантования по уровню, т. е. цена младшего разряда в двоичном коде числа g*(jt0 )

Величина определяется из условия:

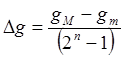              (3.5)

где п — число разрядов  в  двоичном   коде  числа;  gMи    gm- — наибольшее  и наименьшее возможные значения величины gсоответственно.

Число g*(jto), полученное в результате выполнения всех преобразований измеряемой величины в ИИК, вводится в одну из ячеек запоминающего устройства УВМ и в дальнейшем  представляет в машине значение    измеряемой величины x(t) в момент времени t = jt0.

Из изложенного вытекают следующие основные задачи пер­вичной обработки информации в АСУТП:

1)  фильтрация сигнала измерительной информации от слу­чайной помехи (погрешности) e(t);

2)  восстановление значения   измеряемой величины x(t)   по сигналу измерительной информации y(t);

3)  коррекция восстановленных значений измеряемой величины с учетом отклонения условий измерения от номинальных;

4)  восстановление значений измеряемой величины x(t)  при
 т. е. интерполяция и экстраполяция.

Кроме того, необходимо оценить влияние квантования сиг­нала измерительной информации по времени и по уровню на точность его представления, а также рассмотреть методы конт­роля и повышения достоверности исходной информации в АСУТП.

3.2. ВЫБОР РАЗРЯДНОСТИ ПРЕДСТАВЛЕНИЯ ИНФОРМАЦИИ

В УВМ И ЧАСТОТЫ ОПРОСА ИЗМЕРИТЕЛЬНЫХ ПРЕОБРАЗОВАТЕЛЕН.

ИНТЕРПОЛЯЦИЯ И ЭКСТРАПОЛЯЦИЯ СИГНАЛА

В современных УВМ наибольшее распространение получил ре­жим обработки данных с фиксированной занятой [48]. При этом погрешность представления исходной информации, вызванная квантованием по уровню, не превышает по абсолютной величине единицы младшего разряда, определяемой соотношением (3.5). Если задана допустимая относительная погрешность квантова­ния по уровню  то необходимое число разрядов определяется из условия


                                     

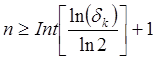
Обычно n>8, так что относительная погрешность квантования по уровню не превышает 0,4%, т. е. является пренебрежимо ма­лой по сравнению с погрешностью измерительного преобразователя.

При разработке АСУТП важен выбор периода t0 квантова­ния по времени сигналов измерительной информации. Эта зада­ча решается с учетом двух противоречивых соображений. С од­ной стороны, увеличение периода t0 снижает загрузку УВМ опе­рациями сбора и первичной обработки исходной информации. В результате большая доля вычислительных ресурсов системы может быть использовала на решение задач контроля и управ­ления более высокого уровня. Это соображение особенно важно для микропроцессорных АСУТП. С другой стороны, при увели­чении периода t0 возрастает погрешность определения действи­тельного значения измеряемой величины y.(t) по решетчатой функции g*(jt0). Эта погрешность проявляется при восстановле-



Рис. 3.2. Схема восстановления непре­рывной функции yф(t) по решетчатой: функции g*(jt0)       



Рис. 3.3. Спектры функций:

а —непрерывной; б, в — решетчатой

при  и при

нии значений функции y(t) в моменты времени, не совпадающие с момен­тами отсчета tj = jt0.

Задачи восстановления непрерывной функции по ее дискретным значениям делятся на задачи экстра­поляции и интерполяции. Экстраполяцией называ­ют определение будущих

значений функции с момента очередного отсчета до момента по­ступления следующего отсчета. Интерполяцией называют опре­деление промежуточных значений функции между двумя полу­ченными отсчетами.

Скачать файл