Алгоритмы первичной обработки информации в АСУТП, страница 13

Уравнения (3.66) выполняются только при подстановке в них истинных значений х_i измеряемых величин. Если же значе­ния измеряемых величин известны с погрешностями Δx_i , т. е.

   (3.67)

где l_j — погрешность выполнения j-го уравнения связи  (3.66), вызванная погрешностями измерения.

Функции fj(x) обычно являются непрерывными и дифферен­цируемыми по всем аргументам, поэтому их можно разложить в ряд Тейлора но степеням величин Δx_i,:

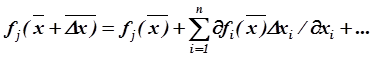  (3.68)

Поскольку при частичных отказах ИИК погрешности Δx_i малы, :можно не принимать во внимание нелинейные члены ряда (3.68), содержащие в качестве сомножителей величины высших порядков (Δx)^k, где k = 2,3,.... Тогда с учетом (3.66) из (3.68) полу­чим:

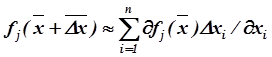        (3.69)

Подстановка уравнения (3.69) в (3.67) дает :

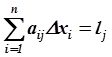        (3.70)

где

На практике расчет параметров a_ij проводят, используя не истинные , а измеренные значения так что

    (3.71)

Система уравнений

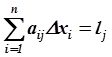
                  (3.72)

является линеаризованной математической моделью объекта управления или некоторой его части. Она служит для расчета оценок погрешностей  Δx_i, которые используют при контроле достоверности исходной информации и диагностике частичных отказов ИИК.

Метод расчета погрешностей Δх, зависит от соотношения между числом измеряемых величин п и числом уравнений связи m.

При п = т значения Δx_i, определяют одним из численных методов решения системы т линейных уравнений (3.72). При п>т можно попытаться уменьшить число рассчитываемых оценок погрешностей с n до т. Для этого результаты измерений q=n—т параметров следует заранее рассматривать как достоверные Если такое допущение правомерно, задача сводится к рассмотренному выше варианту.

В общем случае при п>т оценки погрешностей Δx_i, определяют, решая оптимизационную задачу

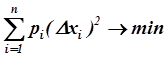             (3.73)

при выполнении соотношений (370). Весовые коэффициенты р<> позволяющие учесть различие в классе точности ИП, рассчиты­вают по формулам [24]

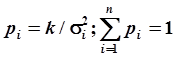            (3.74)

где k = const, σ_i— среднеквадратичная погрешность /-того ИП

Для решения задачи нелинейного программирования (3.73) используют метод неопределенных множителей Лагранжа. Сос­тавляют функцию Лагранжа:

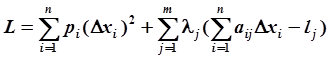
где λ_i = const—множители Лагранжа.

Для нее записывают необходимые условия оптимальности δL/δx_i = 0 и δL/δλ_j=0 в виде следующей системы (n+m) уравне­ний:

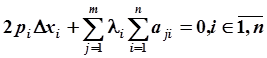              (3.75)

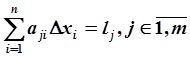                           (3.76)

Искомые оценки погрешностей Δх_i являются решениями систе­мы линейных уравнений (3 75) — (3 76).

Рассчитанные значения оценок погрешностей используют для коррекции результатов измерении

" Среднеквадратичная погрешность откорректированных значений измеренных величин меньше среднеквадратичной погреш­ности измерении ИИК, причем увеличение точности оценок тем значительнее, чем меньше разность п—т

На рис. 3.12 представлена блок-схема алгоритма контроля достоверности исходной информации, диагностики частичных отказов ИИК и коррекции результатов измерений, основанного на использовании функциональных связей между измеряемыми величинами. Он работает следующим образом

После инициации (блок /) в оперативную память УВМ вво­дятся исходные данные (блок 2) к начинается циклический расчет погрешностей l_i уравнений связи по формуле (3.67) для чего служат блоки 4,7 и 8. В блоке 5 рассчитанные значения сравниваются с наибольшими допустимыми значениями l_i^* :

              _(3.78)

Если условие (3.78) выполняется для всех уравнений связи, то все результаты измерения признают достоверными, т.е. и работа алгоритма заканчивается, тах как логическая переменная kсохраняет свое первоначальное значение k = 0.

Нарушение условия (3.78) хотя бы для одного уравнения связи служит признаком наличия частичных отказов. При этом в блоке 6 логическая переменная kприобретает значение 1, и после окончания цикла расчета погрешностей l_j уравнении связи алгоритм переходит к расчету оценок Δx_i,- погрешностей измере­ний (блоки 10—25). Он начинается с циклического вычисления оценок коэффициентов а_ij линеаризованных уравнений связи в блоках 10—16. Коэффициенты рассчитываются по формуле (3.71) в блоке 12. В блоке 17 формируется матрица коэффици­ентов a_ijсистемы линейных уравнений (3.72) и матрица-столбец погрешностей //. Если расчет выполняется для случая п=m, то на этом работа блока 17 заканчивается. Для случая п>т мат­рица, формируемая блоком 17, дополняется строками, соответ­ствующими уравнениям (3.75).