Другие предметы \ Теория автоматического управления

Алгоритмы первичной обработки информации в АСУТП, страница 7


После выполнения соответствующих преобразований получают следующее выражение для дисперсии погрешности фильтрации:

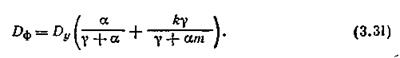
Оптимальное значение параметра настройки у получают из необходимого условия экстремума функции Dф(у):

откуда

Таким образом, функция Dф(у) имеет единственную точку стационарности, тип которой зависит от знака второй произ­водной при y=y0- Можно показать, что при выполнении условия

особая точка является минимумом функции Dф(у), а при выпол­нении условия km<1 в точке y = y° функция Dф(у) достигает максимума Таким образом, если сочетание характеристик по­лезного сигнала и помехи соответствует случаю (3.32а),то опти-мальное значение параметра настройки определяется по форму­ле (3.32). Если это условие не выполняется, то оптимальным является наибольшее допустимое значение параметра у-

При программной реализации экспоненциального фильтра дифференциальное уравнение (3,28) заменяют разностным урав­нением вида


где i — номер цикла расчета.

Отсюда получают следующее рекуррентное соотношение для вычисления сглаженного значения yф(j) в очередном j-том цикле расчета:

К достоинствам алгоритма экспоненциальной фильтрации отно­сятся малая трудоемкость расчетов и Малый объем памяти УВМ, в которой должна храниться величина у и обновляемая в каждом цикле расчета величина yф(j—1).

Фильтр     скользящего     среднего     в   аналоговом    варианте реализует     вычисление    среднего     значения     функции    g(t)




на интервале времени от t—Тф до t(рис. 3.9, б):

где Тф — параметр настройки фильтра (время усреднения).

Преобразуем   правую часть выражения   (3.34),  представив его в виде:

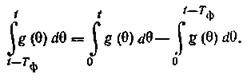
которое  аналогично  по  структуре выражению   (3 12)   и  может быть преобразовано к виду


Отсюда видно, что фильтр скользящего среднего представляет собой параллельное соединение двух интегрирующих звеньев, одно из которых последовательно соединено со звеном запаздывания (рис. 3.9а). Поэтому амплитудно-фазовая характеристика фильтра описывается выражением

Решая совместно (3.24) — (3.27) и (335), можно получить выражение для дисперсии погрешности Dф фильтра скользящего среднего и определить оптимальное значение рф параметра, настройки из необходимого условия минимума функции Dф(Tф). Получаемое при этом выражение очень громоздко, неудобно для практического использования. На его основе рассчитаны номограммы [24], по которым для заданных значений a, m, kможно определить Т°ф.

При программной реализации фильтра скользящего средне­го расчет сглаженного значения уф(j) в очередном j-том цикле проводится по формуле

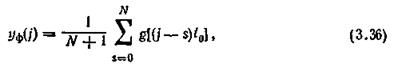
где N—T$,lto— параметр настройки фильтра

Для расчета по формуле (3.36) требуется хранить в памяти УВМ (N+1) значение функции g(jt0).

Статистические фильтры. Статистическими называют фильтры, которые в аналоговом варианте представляют собой параллель­ное соединение (n+1) цепочек, состоящих из усилительного зве-

на интервале времени от t—Тф до t(рис. 3.9, б):

где Тф — параметр настройки фильтра (время усреднения).

Преобразуем   правую часть выражения   (3.34),  представив его в виде:

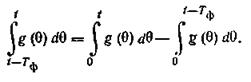
которое  аналогично  по  структуре выражению   (3 12)   и  может быть преобразовано к виду


Отсюда видно, что фильтр скользящего среднего представляет собой параллельное соединение двух интегрирующих звеньев, одно из которых последовательно соединено со звеном запазды­вания (рис. 3.9а). Поэтому амплитудно-фазовая характеристи­ка фильтра описывается выражением

Решая совместно (3.24) — (3.27) и (335), можно получить выражение для дисперсии погрешности Dф фильтра скользяще­го среднего и определить оптимальное значение рф параметра, настройки из необходимого условия минимума функции Dф(Т$). Получаемое при этом выражение очень громоздко, неудобно для практического использования. На его основе рассчитаны номо­граммы [24], по которым для заданных значений a, m, kможно определить Т°ф.

Скачать файл