Алгоритмы первичной обработки информации в АСУТП, страница 3

В общем случае восстановление непрерывного сигнала по решетчатой функции производится формирующим фильтром, представляющим собой линейное динамическое звено с ампли­тудно-фазовой характеристикой (АФХ) (рис. 3.2). Сле­довательно, для восстановленного сигнала справедливо следую­щее соотношение:

где G*(to) —преобразование Фурье функции g*(jt₀).

Из теории импульсных систем известно [55], что спектр ре­шетчатой функции является периодической функцией с периодом, равным частоте квантования

Смещенные компоненты спектра могут частично перекрывать

друг друга, причем степень перекрытия увеличивается по мере, уменьшения частоты  т. е. при увеличении периода квантования t₀ (рис. 3.3). В  результате наложения спектр решетчатой функции искажается, и из него невозможно выделить спектр исходной непрерывной функции. Исключение составляет физически нереализуемый случай, когда спектр непрерывной функции ограничен,

т.е.

                                                   при 

а частота квантования удовлетворяет условию

                        .                            (3.6)

При  этом смещенные компоненты в спектре решетчатой функ­ции g(jt₀) не перекрываются, и из него можно выделить главную несмещенную составляющую, совпадающую со спектром непре­рывной функции g(t) (см. рис. 3.3). Для точного восстановления исходной непрерывной функции по решетчатой функции необходимо использовать идеальный нереализуемый фильтр с АФХ

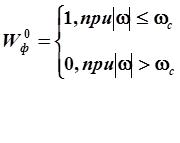
Действительно, погрешность восстановления, очевидно, равна

или в преобразованном по Фурье виде —

                           (3.8)

Для идеального фильтра (3.7) при выполнении условия (3.6) справедливо равенство

                              (3.9)

и, следовательно

Соотношение (3.6) составляет содержание теоремы Котельникова — Шеннона, которая определяет необходимые условия передачи без искажения информации, содержащейся в непрерывном сигнале при его квантовании по времени и последующем восстановлении.

Если для восстановления используют фильтр с АФХ Wф(iω), отличающейся от (3.7), то даже при выполнении условия (3.6) точное восстановление исходной непрерывной функции невозможно. Погрешность восстановления получим, применив обратное преобразование Фурье к выражению (3.8) с учетом (3.9):

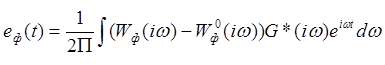      (3.10)

Таким образом, погрешность восстановления зависит от свойств исходной функции g(t), периода квантования t₀ [эти два фактора определяют G*(iω)J и АФХ формирующего фильтра

Рассмотрим наиболее распространенные методы экстраполяции и интерполяции.

Метод ступенчатой экстраполяции (экстраполятор нулевого _v порядка) состоит в том, что значение восстанавливаемой функции y_ф(t) для любого момента времени jt₀<t<(j+l)to принимают равным g*(jt_Q) рис. 3.4):

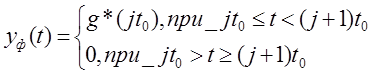             (3.11)

Сигнал, восстановленный по алгоритму  (3.11), можно, очевидно рассматривать как сумму двух направленных в разные стороны скачков с амплитудой g*(//₀), один из которых сдвинут по времени на t₀