Другие предметы \ Теория автоматического управления

Алгоритмы первичной обработки информации в АСУТП, страница 5

Для  решения  поставленной  задачи воспользуемся  неравен­ством [22]:

,                                              (3.17)


где De/D— отношение добавочной дисперсии, связанной с заменой непрерыв­ного случайного процесса ступенчатым с шагом /о, к дисперсии случайного процесса D; A — продолжительность корреляционной функции случайного процесса.

Если бы продолжительность корреляционной функции можно было оценить без построения этой функции, то неравенство (3.17) позволило бы оценить интервал опроса t0. Ниже получим оцен­ку величины А через среднее число нулей случайного процесса N0lт. е. через среднее число пересечений им линии своего ма­тематического ожидания в единицу времени. Предварительно отметим, что рассмотрение процессов с корреляционной функ­цией конечной продолжительности более естественны, чем про­цессов со спектральной плотностью, ограниченной частотой среза, так как первые, в отличие от вторых, физически реали­зуемы.

Известна связь среднего числа нулей NQсо спектральной плотностью случайного процесса S(со):

Пользуясь этой формулой, попытаемся найти минимальную продолжительность корреляционной функции Rg, имеющей за-данное число нулей Л^о. В силу свойств преобразования Фурье, произведение любых двух функционалов, однозначно определяе-мых корреляционной функцией Rg, один из которых имеет раз­мерность времени, а другой — частоты [последний выражается через преобразование Фурье от Rg(i)], не изменяется при сжа­тии или растяжении корреляционной функции, т. е. при измене­нии масштаба времени.

Анализ размерности правой части формулы для N02показы­вает, что среднее число нулей имеет размерность частоты. В ка­честве функционала, имеющего размерность времени, примем

Пользуясь этой формулой, попытаемся найти минимальную 1 продолжительность корреляционной функции Rg, имеющей заданное

 число нулей Л^о. В силу свойств преобразования Фурье, I произведение любых двух функционалов, однозначно определяемых

 корреляционной функцией Rg, один из которых имеет раз­мерность времени, а другой — частоты [последний выражается через преобразование Фурье от Rg(i)], не изменяется при сжа-тии или растяжении корреляционной функции, т. е. при измене­нии масштаба времени.

Анализ размерности правой части формулы для N02показы­вает, что среднее число нулей имеет размерность частоты. В качестве

  функционала, имеющего  размерность времени,  примем

Рис. 3.8. Определение корреляци­онной функции минимальной про­должительности

продолжительность Д кор­реляционной функции Rg(т). Таким образом, произведе­ние C=N0Δ зависит от фор­мы Rg(t) и не зависит от              выбора масштаба времени. Поэтому первоначально зафиксируем Δ=1 и при этом условии будем искать минимум Nо, а точнее Nо2. Чтобы учесть требование ко­нечной продолжительности корреляционной функции, перейдем во временную область. Представим S(ω) в виде |s(ω) |2, что соответствует представлению Rg(f) как свертки двух функций — г+(т) и г-(т), первая из которых определена на интервале (О, 1), а вторая — на интервале (0, —1). Формула для среднего числа нулей может быть теперь переписана в виде


Чтобы найти минимум N20, потребуем, как обычно, минимума числителя при фиксированном значении знаменателя. Задача

: (индекс «+» для краткости записи опущен) решается с исполь­зованием уравнения Эйлера. Составим функционал Лагранжа

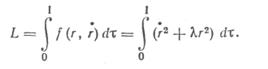
и запишем для него уравнение Эйлера


Его решение (а точнее — множество решений):

Подставив решение в условие для заданной дисперсии, получим5

Величина I на найденных решениях I=D0k2π2; тогда I/DQ=kπ2. Это отношение минимально для k = l. Соответствующее решение

г+(т) показано на рис. 3.8. Там же нанесена корреляционная функция Rg*(т), имеющая при заданном среднем числе нулей минимальную продолжительность.

При Δ=1 величина Cminоказывается равной единице. Следо­вательно, если фиксировано среднее число нулей jV0, то мини­мальная продолжительность корреляционной функции Дт1п=1/Л^о.

Возвращаясь к неравенству (3.17) и подставляя вместо Д значение Δmin, получим оценку сверху для интервала опроса:

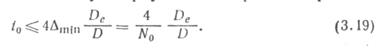
Пример. Пусть относительная дисперсия, спязаппля с дискретностью опроса датчиков, ис должна превышать пяти процентов. По формуле (3.19) имеем для t0 оценку

Скачать файл