Блок 18 предназначен для решения одним из численных методов системы линейных уравнении (3.72) или (3.75) — (3.76). Эта часть алгоритма требует основных затрат машинного времени и оперативной памяти ЭВМ. В результате работы блока 18 получают оценки погрешностей измерений Δxi.
В блоках 19—23 производится диагностика частичных отказов ИИК, для чего оценки Δxi сравнивают с наибольшими допустимыми значениями погрешностей измерений Δxi*:
(3.79)
Нарушение условия (3.79), которое проверяется в блоке 20,
является
признаком частичного отказа i-того ИИК; сообщение об этом формируется
блоком 21. В блоке 22 рассчитывается откорректированное значение xiизмеряемой величины
по формуле
(3.77). Блок 25 служит для вывода результатов расчета, после чего работа
алгоритма завершается. Исходными данными для работы алгоритма являются массивы
следующих величин: измеренных значений параметров 
допустимых
погрешностей lj* уравнений связи; допустимых погрешностей
Δxi* измерений; весовых коэффициентов pi(если n>m).
Пример. Рассмотрим контроль достоверности результатов
измерения расходов
азотной кислоты, поступающей с производства на склад. Производство состоит
из трех параллельно работающих агрегатов. На выходе каждого из них
измеряется расход qt (i
l,3) продукционной кислоты.
Затем
кислота поступает в коллектор, в котором измеряется общин расход q4. Поскольку расход q4является одним из
основных отчетных параметров производства, для его измерения используют расходомер
более высокого
класса точности, чем для измерения расходов q1 –qл Исходные данные для 'алгоритма контроля достоверности исходной информации следующие:
измеренные значения параметров 
=12,l т/ч; 
=11,6 т/ч; 
= 12,4
т/ч; 
=34,5 т/ч;
допустимая погрешность выполнения уравнения связи l*=1,5 т/ч;
допустимые погрешности измерения отдельных параметров Δx1* = Δх2* = Δx3* = 0,45 т/ч; Δx4* = 0,65 т/ч;
среднеквадратичные погрешности измерения σ1=0,3 т/ч; σ2 =0,2 т/ч; σ3= 0,35 т/ч; σ4 = 0,33 т/ч.
Действуем в соответствии с блок-схемой на рис. 3.12.
1. Определим погрешность lвыполнения уравнения связи между измеряемыми параметрами, которое в данном случае имеет вид:
|
|
2. Проверка условия (3.78)
приводит к выводу, что среди результатов^
измерения
х,- имеются недостоверные.
3. Исходное-
уравнение (3.80) является линейным, следовательно, коэф
фициенты
линеаризованного урапнгнпя (3.7(1) совпадают с коэффициентами
уравнения
(3.80):
Для дальнейшего формирования системы уравнении (3.75) — (3.76) необходимо рассчитать весовые коэффициенты /;,-. Запишем условие (3.74) для заданных значении ст,-:
|
|
'•откуда /г = 0,0187; р, = 0,208; р2=0,468; р3 = 0,153; р4 = 0,172. : - Теперь запишем систему уравнении (3.75) — (3.76):
|
|
Ее решениями являются следующие значения оценок погрешностей измерений:
4. Проверим выполнение условия (3.79). Как легко убедиться, оно не выполняется только для параметра q3, из чего следует вывод о частичном отказе этого ИИК.
В заключение рассчитаем откорректированные оценки значений измеряемых величин:
При этих значениях удовлетворяется уравнение связи (3.80).
Изложенный выше алгоритм можно использовать не только для определения частичных отказов ИИК, но и для более глубокой диагностики погрешностей измерения. Для этого подвергают статистической обработке расчетные значения погрешностей Δxi, получаемые в последовательных циклах работы алгоритма. Оценка математического ожидания случайной величины Ai, за N циклов расчета характеризует систематические погрешность измерения t-того ИИК
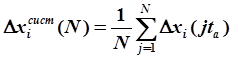
где t— период с которым выполняются расчеты но алгоритму контроля достоверности исходной информации
По формуле
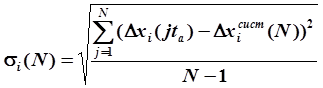
рассчитывают оценку среднеквадратичной погрешности измерения
|
|
|
|
|
|
|
|
|
|
|
|
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
