4.4. Вставьте в рабочий документ п. «4.2. Индивидуальное решение системы нелинейных уравнений. Вариант №___». Решите систему нелинейных уравнений (4.2) вашего варианта (см. Исходные данные – разд. 15.7, табл. 15.7.1) посредством решателя Mathcad Given … Find:
f1(x,
y)= 0, ![]()
f2(x, y)= 0.
Используйте пример рис. 4.1 или 4.2 Задания 4.
Внимание! Решатель Given … Find является локальным оператором: он вычисляет корни системы, соответствующие начальному приближению, и не производит какого-либо поиска дополнительных корней. Чтобы вычислить заданное число корней, нужно для каждого корня найти его приближенное значение посредством упрощенного решения системы с использованием графических средств Mathcad.
Различают два варианта при графическом упрощенном решении системы: когда переменные в уравнении системы можно отделить друг от друга и когда нельзя.
1. Для первого варианта в каждом уравнении одну из неизвестных выражают через другую, строят две кривые на графике, точки пересечения которых и дают приближенные значения корней, которые затем уточняют посредством решателя Given-Find – см. рис. 4.1. Приближенные значения измеряют посредством панельки Trace (щелчок ПКМ на графике-Контекстное меню-Trace).
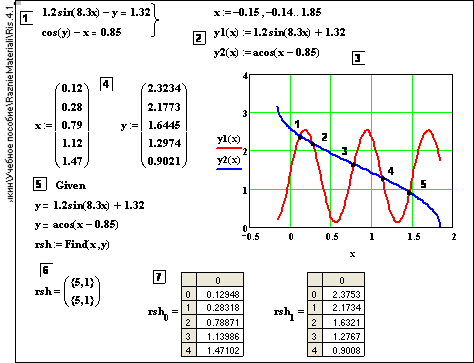
(4.3)
Рис. 4.1. Решение системы уравнений (4.3) с отделяющимися неизвестными (показаны 5 корней системы). 1–исходная система; 2–система с разделенными переменными для построения графика 3; 4–векторы приближенных значений координат корней, определенных через измеритель «X-Y Trace»; 5–решатель системы (4.3); 6–выходная таблица решателя в виде гнездовой матрицы; 7– вывод элементов гнездовой матрицы–координат х и у корней
2. Для второго варианта одну переменную выражают через другую, используя локальный решатель root(…), строят кривые, находят точки пересечения и далее действуют аналогично первому случаю – см. рис. 4.2. Как видно из этапов 4…7, решатель находит корни, отличающиеся от начальных приближений (векторы
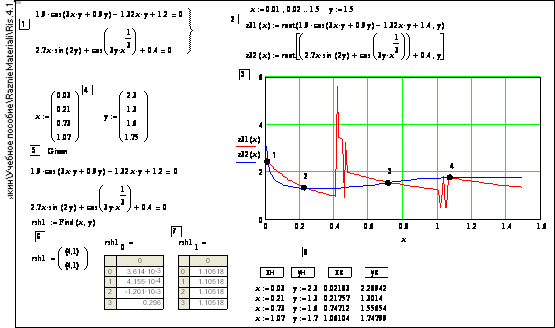
(4.4)
Рис. 4.2. Решение системы уравнений (4.4) с неотделяющимися переменными (показаны 4 корня) системы. Этап 8 – Индивидуальное вычисление корней в точках 1…4 решателем 5: хн, ун – начальные координаты корня, хк, ук – координаты корня, вычисленные решателем
х и у в этапе 4) и лежащие вне исследуемого диапазона (0,01…1,5). Поэтому корни в точках 1…4 графика вычислялись индивидуально на этапе 8: хн, ун – начальные координаты корня (определенные посредством панельки Trace ), хк, ук – координаты корня, вычисленные решателем из этапа 5.
4.5. Вставьте в рабочий документ п. «4.4. Полное сеансовое решение системы 2 нелинейных уравнений методом сканирования по начальным данным с контролем вычисляемых корней по контурной карте системы, Вар.№ (ваш вариант)».
1. Ознакомьтесь с Решением системы нелинейных уравнений Методом сканирование по начальным данным с решателем given-find по разд. 6.3.1 Пособия.
2. Постройте контурную карту заданной системы уравнений согласно Этапам формирования контурной карты разд. 6.3.1.3 и рис. 6.9; нанесите границы области поиска корней и номера всех точек взаимопересечения разноименных контуров, как кандидатов на корни. Если количество определяемых корней больше 30, то их число можно уменьшить в пределах области поиска до 30 с обязательным изменением границ области.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.