Цикл заданий по расчетам в Mathcad (Глава 14 Методики применения пакета Mathcad для решения научных и типовых общетехнических задач), страница 11

Постройте  переходный процесс в САУ  с дифуравнением замкнутой системы (5.1), взятым из п. 5.1 задания,  руководствуясь этапами разд. 7.2.1 и рис. 7.4. Пособия.

5.3.Вставьте в рабочий документ текстовый блок « 5.3. Текущая дата. Решение дифуравнения/системы дифуравнений 1-го порядка (в зависимости от вашего варианта). Кривая (название), вариант №___».

·   Решите дифуравнение или систему дифуравнений решателемrkfixed(…) при начальных условиях: и данных вашего варианта из табл. 15.8.2 разд. 15.8, используя разд. 7.2.1 и 7.2.2  Пособия.

·  Постройте график решения в координатах, руководствуясь графой 7 табл. 15.8.2 и соответствующим рисунком (при его наличии), снабдите график поясняющей надписью.

·  Скопируйте решение и график, установите параметры классической кривой (в конце каждого раздела табл. 15.8.2, за исключением двух последних), проконтролируйте изменение графика.

5.4.Вставьте в рабочий документ текстовый блок « 5.4.  Текущая дата. Решение линейной системы дифуравнений 1-го порядка надежности САУ. Вариант №___».

Решите систему дифуравнений (описывает надежность работы ремонтируемой резервированной САУ) решателемrkfixed(…) при начальных и нормировочном условиях и данных вашего варианта из табл. 15.8.3, используя разд. 7.2.4 Пособия и рис. 5.3 настоящего задания.

·  Постройте график решения в координатах, руководствуясь рис. 5.3, снабдите график аналогичными поясняющими надписями.

Обратите внимание на способ ввода нормировочного условия  – рис. 5.3 и 5.4.

·  Постройте таблицу вычисленных нормированных вероятностей, руководствуясь командами рис. 5.4.

 

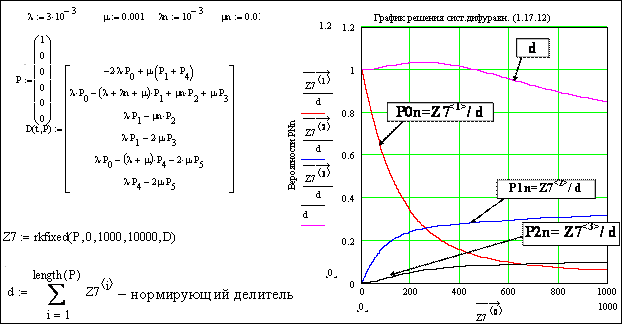
(5.3)    

Рис. 5.3. Решение системы шести дифуравнений. На рисунке – графики первых трех нормированных вероятностей: P0n, P1n и P2n (в РД Mathcad рисунок должен располагаться ниже присвоения d).

Нормировочное условие в случае системы (5.3):

Р₀(t) + Р₁(t) + Р₂(t) + Р₃(t) + Р₄(t) + Р₅(t) = 1,                                                                                        (5.4)

поэтому нормированное значение вероятности, например, Р₀  – Р0n, равно

Р0n(t) = P₀(t) / ( Р₀(t) + Р₁(t) + Р₂(t) + Р₃(t) + Р₄(t) + Р₅(t) ) = Z7^<1>/d.                                                (5.5)

 

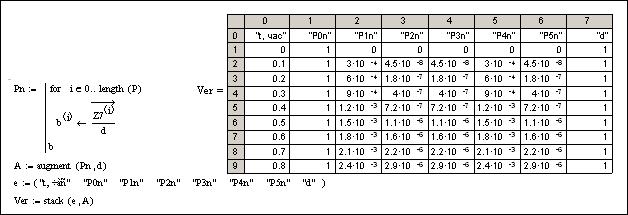
Рис. 5.4. Вывод таблицы нормированных вероятностей решения системы (5.3)

Задание  6

Решение линейных дифференциальных уравнений и систем методом прямого и обратного преобразования Лапласа. Исследование  систем автоматического управления с периодической нелинейностью на границе устойчивости «в большом»

6.1.  Создайте новый рабочий документ в Mathcad для 6-го…8-го заданий, сохранив его в вашей папке под именем «Р6−8МкдФамилия(ваша)».

6.2.  Вставьте в РДМ текстовый блок:

«Задание 6

Текущая дата.  Функциональное решение  дифуравненй и их систем». 

 6.1. Функциональное решение линейного дифуравнения. Вариант №___» 

·  Найдите функциональное решение x(t) вашего преобразованного дифуравнения из п. 5.2 Задания 5 с вычисленными вами начусловиями, используя метод прямого-обратного преобразований Лапласа,  в соответствии с этапами разд. 9.1.

Вычисления производите в новом РДМ, свободном от других вычислений!

·  Скопируйте вычисление переходного процесса вместе с рисунком, выполненным  по п. 5.3 Задания 5, и постройте на рисунке график  найденного решения x(t). Безошибочным выполнением преобразований в предыдущем пункте добейтесь, чтобы график x(t) отличался от ранее построенного не более, чем на 5…10%. Снабдите график соответствующей поясняющей надписью.