Цикл заданий по расчетам в Mathcad (Глава 14 Методики применения пакета Mathcad для решения научных и типовых общетехнических задач), страница 5

  По передаточной функции разомкнутой системы (данные возьмите для вашего варианта из табл. 15.1.2 разд. 15.1) 

 

                                                                                                                                       (2.1)                                                                                                                                             

исследуйте  устойчивость САУ, согласно разд. 2.6.2 Пособия, меняя величину К.

·  Постройте показательную точку (–1, i0) и два годографа: один – устойчивый, причем запас устойчивости по амплитуде D (см. рис. 2.8, В) у него должен быть не более 4 % (для определения запаса используйте измеритель «X-Y Trace» в режиме сканирования по точкам графика: при выделенном графике –Формат-Граф-Трейс; измеренное значение хD должно находиться в промежутке –1…–0,96); другой – неустойчивый, по вашему усмотрению (см. исходные формулы (2.9) и построения на рис. 2.8. Пособия).

·  По измеренному хD (измерения производите на увеличенном участке графика, аналогичном рис. 2.1) вычислите запас устойчивости D по формуле (2.2) и вставьте наименование единицы измерения – %.

(2.2)

 

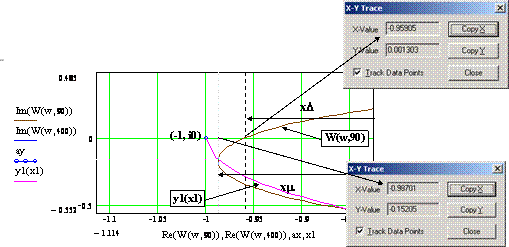
Рис. 2.1. Определение  исходных данных хD и хm для вычисления запасов

                         устойчивости по амплитуде D и фазе m для САУ с                   

·  На вашем графике постройте также нижнюю полуокружность единичного радиусаy1(x1), используя формулы (2.3) – см. рис. 2.1.

(2.3)

·  По точке пересечения полуокружности с устойчивым годографом W(w,К) посредством X-Y-Trace измерьтеxm (см. рис. 2.1) и вычислите запас устойчивости по фазе m посредством формулы (2.4) вставьте наименование единицы измерения – град.

 

(2.4)

                                  , град

2.3.  Вставьте новый пункт «2.2. Текущая дата. Решение уравнений. 2.2.1. Полиномиальное уравнение. Вариант №___». Решите уравнение(2.5), используя оператор polyroots(v), согласно разд. 5.1.1 Пособия.

                           а6×х⁶ + а5×х⁵ + а4×х⁴ + а3×х³ + а2×х² + а1×х + а0 = 0.                                                                (2.5)

Данные, согласно вашему варианту, – в разд. 15.4 Пособия (табл. 15.4.1).                       

2.4.  Вставьте новый пункт «2.2.2. Текущая дата. Исследование уравнения. Вариант №___». Проведите исследование уравнения (2.6) (т.е. определите зависимость корней уравнения от векторных параметров р1 и р2 при квазирядном способе сочетания их значений) на основе методики разд. 5.1.3, рис. 5.4 с формированием полной таблицы ИТИ.

                                  Р4×а4×х⁴ + Р3×а3×х³ + Р2×а2×х² + Р1×а1×х + Р0×а0 = 0                                                     (2.6)

Данные к уравнению, согласно вашему варианту, – в разд.15.4 Пособия (табл. 15.4.2 и 15.4.3), причем, коэффициенты выражаются через параметры р1и р2 с использованием численных значений  Р4…Р0 и табл. 15.4.2. Озаглавьте полученную таблицу.