Упрощённый расширенный Евклидовый алгоритм продолжает тестировать новое b, пока не найдёт gcd(m, b) = 1, и его мультипликативный инверсный модуль m. Отметим, что в упрощённой версии были удалены переменные A1, B1 и T1 потому, что они не относились к вычислениям. Взамен допустимых T2 <= A2 - Q*B2 было использовано T2 <= A2 + Q*B2. Таким образом можно гарантировать, что T2 всегда является положительным. Это делает обеспечение деталей более простым, потому что нет необходимости иметь дело с отрицательными числами. Данными исходными значениями A2 и B2 являются 0 и 1, соответственно, легко заметить, что T2, вычисленное упрощённой версией, является величиной T2, вычисленной обычной версией. Когда В3 эквивалентно 1, В2 определённо положительно. Таким образом, оставляя его величину является достаточным для правильного выходного сигнала.
Другим отличием в упрощённом алгоритме является то, что замещается T3 <= A3 mod B3 на T3 <= A3 - ëA3/B3û * B. Очевидно, что A3 mod B3 = A3 - ëA3/B3û * B3. Был спланирован делитель, который берёт большое делимое и маленький делитель и возвращает большое частное и маленький остаток. Потому что в этом отдельном приложении, где мы имеем дело с большим m( приблизительно 1024 бита) и маленьким b( меньше 12 бит, описанном раньше), делитель используется только в первом делении. Остальные операции деления имеют дело с числами меньше, чем b, простой алгоритм вычитания со сдвигом выполняет задачу. Чтобы сделать действительное b быстрее, предварительно вычисляются все простые числа меньше 2000, исключая 2. Потому что результат всех этих простых чисел больше, чем 21024, что значит, что любое m меньшее 21024 стоит впереди наименьшего из этих простых чисел. Эти простые числа жёстко запрограммированы на встроенном блоке памяти( так называемом простом числе ROM). Fetch_new_b в упрощённом алгоритме означает следующее простое число, выбранное во время запроса.
Расширенный Евклидов алгоритм не использует какие-либо арифметические операции с модулем. Взамен он требует регулярного множителя для вычисления Q*B2. Был выполнен 1024-битный умножитель с использованием алгоритма умножения со сдвигом к плюсу.
Внешний вид GCD компонента с использованием упрощённого расширенного Евклидова алгоритма представлен на рисунке 8.
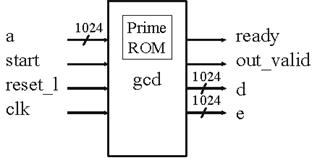
Рисунок 8 - GCD компонент с использованием упрощённого расширенного Евклидова алгоритма.
3.7 ГЕНЕРАТОР СЛУЧАЙНЫХ ЧИСЕЛ
Линейный регистр сдвига с обратными связями( LFSR) использован для генерации псевдо случайных чисел. В частности, Фибоначчи LFSR был выполнен, т.к. он более удобен для обеспечения деталей, чем Гелиос LFSR. Теоретически n-битный линейный регистр сдвига с обратными связями может генерировать случайную последовательность длиной (2n - 1)-бит перед повторением. Не смотря на это, LFSR с максимальным периодом должен удовлетворять следующей особенности: полином, сформированный из элемента последовательности, плюс постоянная 1, должен быть простым полиномом по модулю 2 [10].Нет возможности найти простой полином для 512-битного LFSR, поэтому был выполнен 521-битный LFSR и использовалось его минимальное значения 512 бит для генерации 512-битных псевдо случайных чисел. Простой полином для 512 бит LFSR был получен из [12], x512 + x32 + 1. Для того, чтобы получить 1024-битное n (n = q*p, где p, q – простые числа), первые два бита случайных чисел были помещены в 1, которая гарантирует, что первый бит n всегда 1(поэтому n – 1024-битное число). Рисунок 9 показывает структуру 521-битного LFSR, 512-битный генератор случайных чисел, выполненный с использованием 512-битного LFSR, представлен на рисунке 10.
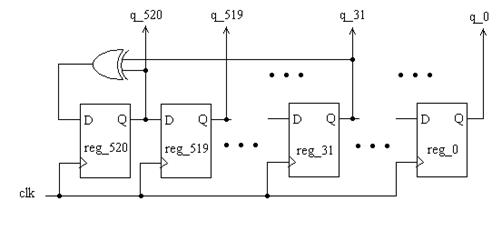
Рисунок 9 – Структура 521-битного LFSR.
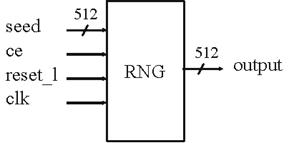
Рисунок 10 – 512-битный генератор случайных чисел.
3.8 ЦИКЛИЧЕСКИЙ УМНОЖИТЕЛЬ
Чтобы вычислить n и j(n) из p и q, необходим циклический умножитель. Был выполнен 1024-битный умножитель с использованием простого алгоритма со сдвигом к плюсу.
3.9 FIFO
Для генерации 12-входного крайнего FIFO и 12-входного простого FIFO была использована Xilinx Core Generator System (Система Генерации Основной части Xilinx).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.