Основная часть RSA обеспечения, как рациональные арифметические операции по модулю, которые включают в себя сложение по модулю, вычитание по модулю, умножение по модулю и возведение в степень по модулю. RSA также содержит некоторые систематические арифметические операции, такие как систематическое сложение, вычитание и умножение, используемые для вычисления n и j(n), и систематическое деление, используемое в GCD операции. Мы обеспечили большую часть упомянутых операций, кроме систематического вычитания, сложения по модулю и вычитания по модулю. Взамен мы используем систематический сумматор, чтобы сделать вычитание, представляя операнды в виде двойного множества. Метод Омуры [6] применяется для рационального вычисления сложения по модулю. В его методе допускается больший рост временного значения n, но меньший, чем 2k (2k-1 < n < 2k), коррекция выполнена, когда временное значение превышает 2k . Техника для возведения в степень по модулю, умножения по модулю, сложения по модулю и операций сложения суммируется в [7], которое мы находим очень полезным.
3.2СЛОЖЕНИЕ.
Сложение является базовым действием, используемым во всех других операциях. Скорость операции сложения играет важную роль во всей системной производительности. Прошлый опыт проекта CS536 говорит нам, что n-битный сумматор, выполненный на FPGA, использующий технологию предварительного просмотра в схеме ускоренного переноса, медленный и расточительный в плане ресурсов. Это потому, что Xilinx FPGA используют 4-ввод информации в обращении к таблице(LUT), чтобы обеспечить любой 4-ввод информации комбинаторной логики. Функции переноса с большим количеством вводов информации нарушен, из-за подхода в несколько 4-вводов информации LUT, делая критическую фазу дольше. Мы использовали Xilinx Core Generator систему для генерации 32-битного сумматора и обеспечили наши собственные 512-битный и 1024-битный сумматоры объединением 16 и 32 32-битных сумматоров, соответственно. Система Xilinx Core Generator делает всё возможное для Xilinx FPGA структуры и создаёт более быстрый 32-битный сумматор.
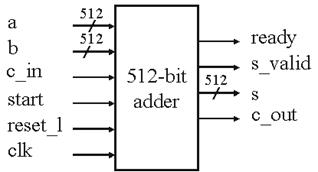
Рисунок 4 – 512-битный сумматор.
Рисунок 4 показывает внешний вид 512-битного сумматора. Ready, start и s_valid – сигналы подтверждения установления связи, указывающие, когда сумматор не занят, когда начинается вычисление, и, когда результат становится верным. 512-битный сумматор имеет 16-часовой циклы задержки. Для 1024-бтного сумматора задержка составляет 32-часовых цикла.
Чтобы вычесть b из a, используя сумматор( в этом случае ввод информации a всегда больше, чем b), мы вводим b и заносим 1 в c_in, результирующее s равно (a - b).
3.3 УМНОЖЕНИЕ ПО МОДУЛЮ
Данные сумматоры, которые были сконструированы для умножения по модулю, используют умножение со сдвигом в плюс. Допустим, A и B – оба k-битные целые числа, соответственно. Допустим, Ai и Bi - i-тый бит A и B, соответственно. Данный алгоритм выглядит следующим образом:
Input: A, B, n
Output: M = A*B mod n
for i = 0 to k-1
if Bi = 1
M <= (M + P) mod n;
end if
P <= 2*P mod n;
end for
return M;
Для 512-битного умножителя по модулю входные сигналы A и B оба 512-битные. Однако, B могло бы быть маленьким числом с множеством впереди стоящих нулей. В осуществлении снабжения деталей перед получением в повторениях сдвига к плюсу, мы ищем позицию с впереди стоящей 1 в B и помещаем в эту позицию (k - 1). Делая это, мы уклоняемся от ненужного сдвига и операций по модулю, делая умножение быстрее, когда B маленький. Как было отмечено раньше, был использован метод Омуры для коррекции частичного продукта М и временного значения P, когда любой из них становится больше 2512. Откорректированные М и Р могут быть до сих пор больше n, поэтому перед возвращением М, будет произведена последняя коррекция М, чтобы убедиться, что М меньше n. Рисунок 5 показывает внешний вид 512-битного умножителя по модулю. 1024-битный умножитель был выполнен таким же образом.
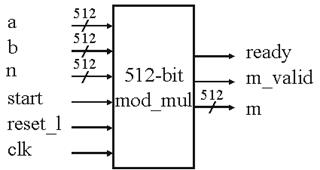
Рисунок 5 – 512-битный умножитель по модулю.
3.4 ВОЗВЕДЕНИЕ В СТЕПЕНЬ ПО МОДУЛЮ
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.