Названа в честь математиков-криптологов Рона Ривеста (Ronald Linn Rivest), Ади Шамира (Adi Shamir) и Лена Адлемана (Leonard Max Adleman) из Масачуссетского Технологического Института, разработавших алгоритм в 1977 году.
Система RSA основана на трудности задачи разложения на множители. Для её использования нужно сгенерировать два больших простых числа p и q, а затем найти N = pq. Потом нужно выбрать не очень большое e (порядка 10 000), взаимно простое с φ(N) = (p − 1)(q − 1) и сгенерировать d, такое, что ed = 1 (mod φ(N)). Далее e и N публикуются (открытый ключ), а числа d, p и q держатся в секрете (секретный ключ). Тот, кто хочет зашифровать сообщение, вычисляет y = xe (mod N) (где x — исходное сообщение) и посылает его владельцу секретного ключа. Тот расшифровывает сообщение по формуле x = yd (mod N).
Способы выбора p и q
Для обеспечения стойкости системы RSA (p − 1) и (q − 1) не должны разлагаться лишь на маленькие простые множители. Обычно выбирают p = rs + 1, где r — другое большое простое число. Кроме того, есть более простые способы проверки на простоту числа p в этом случае.
Длина ключа
Число N должно иметь размер не меньше 512 бит. В настоящий момент (2006 год) система шифрования на основе RSA считается надёжной, начиная с размера N в 1024 бита.
Применение RSA
Система RSA используется для защиты программного обеспечения и в схемах цифровой подписи. Также она используется в открытой системе шифрования PGP.
3.1 ВВЕДЕНИЕ В ПОСТРОЕНИЕ RSA
В этом проекте ставится под вопрос выполнение полнофункциональной 1024-битной RSA схемы на FPGA, включая ключ генерации и данные кодирования. Также желаема высокая производительность, мы пытаемся добиться высокой системной частоты, маленькой области чипа и низкой мощности. Мы дали им более высокий приоритет, чем производительности с тех пор, как RSA схема выполнена в ресурсо - ограниченном FPGA, возможно разделённом остальными модулями. Мы выполнили полно-функциональную RSA схему, включая ключ генерации и данные кодирования, на VHDL.
RSA алгоритм был инвертирован Rivest, Shamir и Adleman 1977 году и опубликован в 1978[5]. Это один из простейших и широко используемых ключей криптографической системы.
Таблица 1 – Суммирование RSA алгоритма.
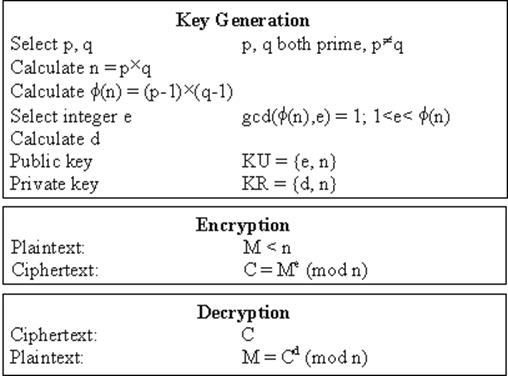
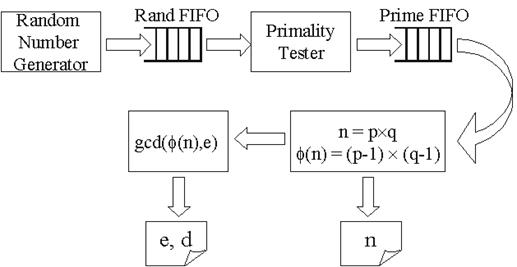
Рисунок 1 – RSA алгоритм.
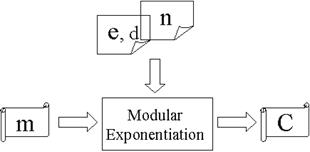
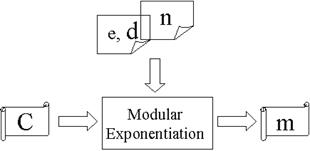
Рисунок 2 – Системная архитектура для ключа генерации RSA.
Системная архитектура для ключа показана на рисунке 2. Генератор случайного числа генерирует 512-битные псевдо случайные числа и сохраняет их на границе FIFO. Когда FIFO заполняется, генератор случайного числа прекращает работу, пока случайное число не будет вытащено тестером на простые числа. Тестер на простые числа берёт случайное число за входной сигнал и тестирует его на простоту. Подтверждённые простые числа перебрасываются в простое FIFO. Так же как генератор случайных чисел, тестер простых чисел начинает новый тест, только когда простое FIFO не заполнено. Большое количество энергии экономится с использованием двух FIFO, т.к. вычисления выполняются только по необходимости. Когда новая пара ключей назначена, нижний поток компонентов выкидывает два простых числа из FIFO и высчитывает n и j(n). N запоминается в регистре. j(n) посылается в GCD( Наибольший Общий Делитель), общая экспонента е выбирается из условия gcd(j(n), e) = 1, а неизвестная экспонента d получена путём инвертирования е по модулю j(n). Е и d также запоминаются в регистрах.
Если n, d и e сгенерированы, RSA кодирование/декодирование становится просто модульной операцией по возведению в степень. Рисунок 3 показывает структуру RSA кодирования/декодирования в детальном исполнении.
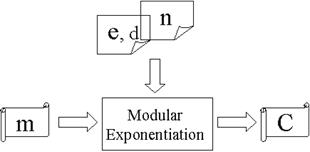

Рисунок 3 – Структура кодирования/декодирования RSA
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.