Проектирование специализированного микроконтроллера, реализующего полнофункциональную RSA схему шифрования, страница 4

Операция возведения в степень по модулю является просто операцией по возведению в степень, где интенсивно сделано умножение по модулю.

512-битный и 1024-битный компоненты возведения в степень по модулю были выполнены с использованием LR бинарного метода, где LR стоит для сканирования направления слева направо экспоненты. Следующий псевдо код описывает бинарный алгоритм LR.

Input: A, B, n

Output: E = A^B mod n

E <= 1;

for i = k-1 to 0

   if B_i = 1

      E <= A*E mod n;

   end if

   if i ¹ 0

      E <= E*E mod n;

   end if

end for

return E;

Также для умножения по модулю, ищется позиция впередистоящей 1 для экспоненты B и ставится (k - 1) для этой позиции. Это отменяет ненужную операцию возведения в квадрат по модулю. Для маленьких экспонент таких, как общая экспонента е, возведение в степень по модулю на много быстрее, чем большой экспоненты такой, как независимая экспонента d. Рисунок 6 показывает внешний вид 512-битного компонента возведения в степень по модулю.

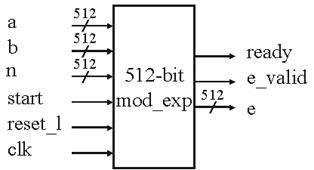
Рисунок 6 - 512-битный компонент возведения в степень по модулю.

3.5 ТЕСТЕР НА ПРИЗНАК ПРОСТОТЫ ЧИСЛА

Признак простоты числа – важная часть ключа генерации RSA. Был выполнен алгоритм, разработанный Миллером и Рэбином[8, 9]. Он использует теорему Ферма, которая устанавливает a^n-1 mod n = 1, если n в начале. Алгоритм Миллера и Рэбина на признак простоты числа такой[10]:

Test (n)

Find integer k, q, with k > 0, q odd, so that (n-1= 2^kq);

Select a random integer a, 1 < a < n - 1;

if a^q mod n = 1 or  n - 1

   return "inconclusive";

end if

for j = 1 to k - 1

   if a^{q2^j} mod n = n - 1

      return "inconclusive";

   end if

end for

return "composite";

Чтобы сделать обеспечение деталей надлежащим образом эффективным, вышеупомянутый алгоритм установлен немного отличным от того, что в книге. Чтобы получить простое число с большой вероятностью( больше, чем 0.999999), случайное число n вычисляется как простое, если TEST возвращает 10 удачных «нерезультативных»[10]. В соответствии с описанием простых чисел всреднем каждая 142-ая попытка (0.4ln(2⁵¹²))  найдёт простое число. Внешний вид тестера по признаку на простоту числа представлен на рисунке 7. Rd_en и rd_ack  - сигналы, подтверждающие установления связи с границей FIFO. Тестер на признак простоты числа заставляет rd_en считывать случайное число с границы FIFO, который затем активирует rd_ack, когда появляется случайное число на шине rand_in.

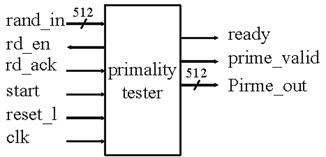
Рисунок 7 - Тестер на признак простоты числа.

3.6 GCD

После того, как получена j(n), необходимо найти маленькое число е с gcd(j(n),e) = 1, которое показывает, что е является простым числом, соответствующим j(n), и его мультипликативный инверсный соответствует j(n). Расширенный Евклидовый алгоритм был выполнен для нахождения gcd(j(n),e), если gcd является 1, то е и его мультипликативная инверсия d возвращаются. Следующий псевдо код показывает расширенный Евклидовый алгоритм в книге [10]. Алгоритм был упрощён при помощи перемещения ненужных переменных и вычислений и сделан более удобным для обеспечения деталей.

Extended Euclid (m,b)

(A1, A2, A3) <= (1, 0, m); (B1, B2, B3) <= (0, 1, b);

loop: if B3 = 0

   return A3 = gcd(m,b);

end if

if B3 = 1

   return B3 = gcd(m,b);B2 = b^-1 mod m;

end if

Q <= ëA3/B3û;

(T1, T2, T3) <= (A1 -  Q*B1, A2 -  Q*B2, A3 - Q*B3);

(A1, A2, A3) <= (B1, B2, B3); (B1, B2, B3)<=(T1, T2, T3);

goto loop;

Simplified Extended Euclid (m,b)

start: (A2, A3) <= (0, m); (B2, B3) <= (1, b);

loop: if B3 = 0

  b <= fetch_new_b;

         goto start;

end if

if B3 = 1

  return (B3, B2);

end if

Q <= ëA3/B3û; T3 <= A3 mod B3;

T2 <= A2 + Q*B2;

(A2, A3) <= (B2, B3); (B2, B3) <= (T2, T3);

goto loop;