БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ
УНИВЕРСИТЕТ ТРАНСПОРТА
Кафедра микропроцессорной техники и информационно-управляющих систем
Н.В. Рязанцева
КЛАССИФИКАЦИЯ ОБЪЕКТОВ С
ИСПОЛЬЗОВАНИЕМ ТЕОРИИ
РАСПОЗНАВАНИЯ ОБРАЗОВ
Методические указания для самостоятельных занятий по подготовке к лабораторным работам
Часть I
Гомель 2002
БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ
УНИВЕРСИТЕТ ТРАНСПОРТА
Кафедра микропроцессорной техники и информационно-управляющих систем
Н.В. Рязанцева
КЛАССИФИКАЦИЯ ОБЪЕКТОВ С
ИСПОЛЬЗОВАНИЕМ ТЕОРИИ
РАСПОЗНАВАНИЯ ОБРАЗОВ
Методические указания для самостоятельных занятий по подготовке к лабораторным работам
Одобрены советом электротехнического факультета
Белорусского государственного университета транспорта
Часть I
Гомель 2002
УДК
Н.В. Рязанцева
Классификация объектов с использованием теории распознавания образов: Метод. указания для самостоятельных занятий по подготовке к лабораторным работам по курсу «Техническая кибернетика»/ Белорус. гос. ун-т трансп. - Гомель: БелГУТ, 2002.- с.
Методические указания содержат краткие сведения по основным понятиям и задачам теории распознавания Описаны методы распознавания образов с использованием обучающей последовательности и условия их применимости, а также методы автоматической классификации. Работа предназначена для студентов электротехнического факультета специализации «Микропроцессорные информационно-управляющие системы» для подготовки к выполнению лабораторных работ по дисциплине «Техническая кибернетика».
Р е ц е н з е н т - кандидат технических наук Шишаков М.Л.
© Н.В. Рязанцева, 2002
Распознавание образов можно представить как процесс принятия решения, устанавливающего принадлежность распознаваемого объекта к некоторому классу путем сравнения определенных его характеристик с характеристиками ранее изученных объектов.
Основными понятиями теории распознавания являются: объект, признак, класс, решающее правило, решающая функция. Каждому объекту соответствует n- мерный вектор, то есть объект можно рассматривать как точку в n- мерном признаковом пространстве (рис.1).
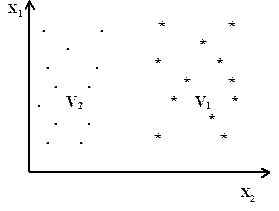
Рисунок 1 - Двумерное признаковое пространство
Каждому классу Vi соответствует некоторая область признакового пространства. Задача распознавания заключается в построении на основе имеющейся информации решающего правила R(X), позволяющего по заданным значениям признаков определить принадлежность объекта к какому-либо классу. Допустимы различные способы описания R(X), но чаще всего R(X) конструируется с использованием решающих функций G(X), которые задают описание классов на языке признаков. Далеко не всегда G(X) можно записать в аналитическом виде, тогда обращаются к алгоритмическому представлению, которое является правилом (алгоритмом) определения значения решающей функции по ее аргументу X.
Целью работы: является изучение формализованной постановки задачи распознавания, условий применения и сути методов ближайшего соседа и К- ближайших представителей, практическое освоение методов компьютерной реализации методов алгоритмического задания решающих функций, применяемых для принятия решений в детерминированных системах распознавания.
Рассмотрим простой пример алгоритмического задания G(X), который получил название алгоритма Фикса-Ходжеса или метода ближайшего соседа.
Правило ближайшего соседа. Этот метод является наиболее простым методом классификации объектов.
Суть метода заключается в следующем: ищется ближайшая к распознаваемому объекту точка из обучающей последовательности; объект Zi относят к классу, к которому принадлежит эта точка.
Таким образом, в основе решения этой задачи лежит понятие расстояния между объектами - точками признакового пространства. В зависимости от свойств объектов и исследуемого процесса могут быть использованы различные формализованные определения расстояния между точками
Z1 (X11, X21, X31, ..., Xn1 ) и Z2 ( X12, X22, X32, ..., Xn2)
Наиболее распространенными являются следующие определения:
r1 – евклидово расстояние
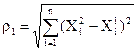 ,
( 1 )
,
( 1 )
r2 –расстояние по Манхэттену
![]() ,
( 2 )
,
( 2 )
r3 - Чебышевское расстояние
![]() (
3 )
(
3 )
Здесь через ![]() обозначена
i-я составляющая j-го вектора.
обозначена
i-я составляющая j-го вектора.
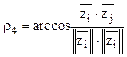 ,
( 4 )
,
( 4 )
В практических задачах адекватный вид r выбирается на основании исследования физической сущности задачи. Конкретные условия могут потребовать составления иных, отличных от (1-3) соотношений.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.