Рассмотренная процедура выполняется до тех пор, пока останется m точек, которые и следует считать эталонами ( центрами) полученных кластеров.
При неизвестном числе классов момент прекращения процедуры объединения можно определять следующим образом.
На каждом к-ом шаге объединения определяется суммарное расстояние между всеми точками
![]()
![]() .
.
Это расстояние будет уменьшаться на каждом шаге на величину
![]() .
.
Резкое увеличение (скачок) величины ![]() на очередном шаге связано с объединением
удаленных скоплений точек, т. е. потерей информации о различии классов. При
появлении такого скачка процедура объединения прекращается, и в качестве ее
результатов берется классификация, полученная на предыдущем шаге.
на очередном шаге связано с объединением
удаленных скоплений точек, т. е. потерей информации о различии классов. При
появлении такого скачка процедура объединения прекращается, и в качестве ее
результатов берется классификация, полученная на предыдущем шаге.
Написать программу, позволяющую классифицировать объекты методом объединения.
Для проверки работоспособности программы по своему варианту (номер в журнале) ввести исходные данные, распечатать листинг программы, таблицу исходных данных и результатов. При выполнении задания к значениям X1 в четных вариантах 1 прибавляется 1, в нечетных - отнимается 1 . К значениям X2 в 2 четных номерах прибавляется 1.
5. Смоделировать распознающую систему , написать и отладить программу для классификации объектов с произвольными значениями признаков. Программа должна запрашивать у пользователя значения обучающей выборки (или читать их из файла), выдавать на экран или принтер исходные данные и результат классификации.
6. Для проверки работоспособности программы по своему варианту (номер в журнале) ввести исходные данные, распечатать листинг программы, таблицу исходных данных и результатов. При выполнении задания к значениям X1 в четных вариантах 1 прибавляется 1, в нечетных - отнимается 1 . К значениям X2 в 2 четных номерах прибавляется 1.
7. Сделать выводы о применимости метода.
8. Оформить отчет, в котором привести листинг программы, копии экранов и результаты работы программы. Сделать выводы о применимости метода.
Наименование и цель работы; основные положения кратких сведений из теории; индивидуальное задание, в котором привести листинг программы, копии экранов и результаты работы программы. Вывод по работе.
Контрольные вопросы
1. Какой из рассмотренных методов более трудоемкий – метод объединения или простейший алгоритм выявления кластеров?
2. Примените метод объединения к множеству данных, приведенному в задаче 2 предыдущего параграфа.
3.
Для задачи 2 вычислите ![]() суммарного расстояния между точками на
каждом шаге объединения. Убедитесь, что оптимальное число классов равно двум,
так как объединение всех точек в один класс вызывает резкое возрастание
величины
суммарного расстояния между точками на
каждом шаге объединения. Убедитесь, что оптимальное число классов равно двум,
так как объединение всех точек в один класс вызывает резкое возрастание
величины ![]() по сравнению с предыдущими шагами.
по сравнению с предыдущими шагами.
Цель работы: Изучить метод алгоритма m внутригрупповых средних, выявить преимущества и недостатки метода. Написать программу, позволяющую классифицировать объекты методомm внутригрупповых средних .
1 Краткие сведенья из теории
Алгоритм m внутригрупповых средних основан на минимизации критерия качества Q и заключается в следующем.
1. Выбираются произвольно m исходных центров кластеров
![]()
2. На к-м шаге алгоритма все объекты распределяются по кластерам по правилу
![]() если
если ![]() <
< ![]() , j=1,2,…,m;
, j=1,2,…,m; ![]() ,
,
где Vi(k) – кластер, центром которого является ![]() .
.
3.
Выбираются новые центры кластеров ![]() , чтобы минимизировать сумму квадратов расстояний
между объектами, принадлежащими Vj(k), и новым центром кластером, т. е. В качестве
, чтобы минимизировать сумму квадратов расстояний
между объектами, принадлежащими Vj(k), и новым центром кластером, т. е. В качестве ![]() берется выборочное среднее, определенное по
множеству точек, входящих в Vj(k):
берется выборочное среднее, определенное по
множеству точек, входящих в Vj(k):
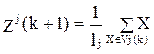 , j=1,2,…,m.
, j=1,2,…,m.
4. Если ![]() = Z(k),
то алгоритм заканчивает работу, иначе он повторяется с шага 2.
= Z(k),
то алгоритм заканчивает работу, иначе он повторяется с шага 2.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.