Классификация объектов с использованием теории распознавания образов: Методические указания для самостоятельных занятий по подготовке к лабораторным работам по курсу «Техническая кибернетика», страница 4

В качестве меры близости точки и класса можно использовать следующее представление:

r ( Z;V_i)= r (Z;Z_э)

где Z- объект, подлежащий классификации, Z_э  -эталонный объект

(эталон) соответствующего класса.

(1)

Координаты эталона рассчитываются по формуле

где Kj- число объектов обучающей последовательности j –го класса, 

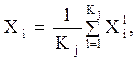X_i –i-я координата эталона, X_i^j – i-я координата  l-той точки j-го класса.

Метод эталона позволяет резко сократить объемы хранимой информации объемы вычислительной работы при распознавании объектов за счет построения разделяющей границы между классами и формировании на ее основе аналитического выражения для решающего правила.

Алгоритм построения разделяющей границы между классами и методом эталона заключается в следующем:

1. Для каждого класса по формуле (1) рассчитывается эталон - наиболее типичный представитель класса.

2. Все признаковое пространство делится на две части гиперповерхностью, все точки которой одинаково отстоят от эталонов.

Распознавание объектов можно производить без построения разделяющей границы на основании сравнения расстояний от исследуемой точки до эталона. В этом случае в памяти необходимо хранить только эталоны и вычислить всего два расстояния.

Линейная разделяющая граница  (гиперплоскость) между классами имеет вид:

                        g(X) = C₀ + C₁ ^. X₁ + C₂ ^. X₂ + . . . + C_n ^. X_n = 0,

где X₁,X₂, . . . , X_n - координаты текущей точки гиперплоскости, С_i  - весовые коэффициенты.

Для удобства записи и вычислений точку доопределяет нулевой координатой X₀, тождественно равной 1. Тогда g(X) можно представить  в виде

На основании g(X) легко формируется решающее правило:

                                         0, если g(X) > 0

                        R(X)                                                                                      ( 2 )

                                         1, если g(X) £ 0

Z Î V₁, если R(X) = 0 и Z Î V₂, если R(X) = 1.

Процедуру расчета разделяющей границы рассмотрим на конкретных примерах.

Пример 1 0бучающая последовательность точек задана таблицей 4. Требуется построить разделяющую границу между классами и определить принадлежность точки Z( 3;4 ) к классам без применения “разделяющей границы” и с ее помощью.

                       Таблица 4 - 0бучающая последовательность

Найдем координаты эталона первого класса:

X_1Э1 = ( 1 + 0 + 2 ) / 3 = 1          X_2Э1 = ( 3 + 1 + 2 ) / 3 = 2,

Тогда Z_Э1( 1; 2 ). Аналогично определим второй эталон.

Z_э2 =(5;4)

X₂

                                                          Э₂

                                  М

               Э1

 

       0                                                                       X₁                                                                           

Найдем координаты середины отрезка Э₁ Э₂ (точки М):

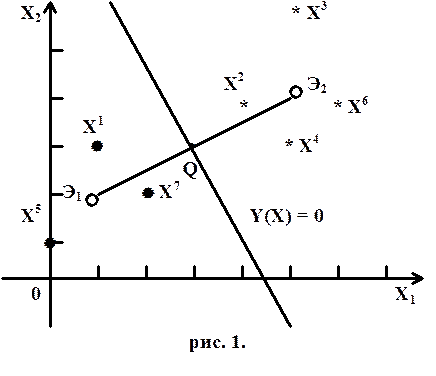
Разделяющая граница между классами V₁ и V₂ проходит через точку M перпендикулярно прямой Э₁Э₂ ,  и имеет вид:

                                  g(X) = C₀ X₀+ C₁ X₁ + C₂X₂ = 0                              (3)

Вектор Э₂Э₁ определяет коэффициенты С₁ и С₂ (из условия ортогональности прямых). Координаты вектора Э₂Э₁  :  С₁ = 1 - 5 = 4 и С₂ = 2 - 4 = -2.

Уравнение (3) принимает вид:

                                  C₀ X₀ - 4 X₁ - 2 X₂ = 0                                       (4)