Качество работы рассмотренного алгоритма зависит от выбора исходных центров кластеров и их числа, а также от геометрических особенностей данных. Поэтому в большинстве случаев практическое применение алгоритма mвнутригрупповых средних требует проведения экспериментов, связанных с выбором расчетных значений параметра m и исходного расположения центров кластеров.
Написать программу, позволяющую классифицировать объекты методом m внутригрупповых средних .
Для проверки работоспособности программы по своему варианту (номер в журнале) ввести исходные данные, распечатать листинг программы, таблицу исходных данных и результатов. При выполнении задания к значениям X1 в четных вариантах 1 прибавляется 1, в нечетных - отнимается 1 . К значениям X2 в 2 четных номерах прибавляется 1.
9. Смоделировать распознающую систему , написать и отладить программу для классификации объектов с произвольными значениями признаков. Программа должна запрашивать у пользователя значения обучающей выборки (или читать их из файла), выдавать на экран или принтер исходные данные и результат классификации.
10. Для проверки работоспособности программы по своему варианту (номер в журнале) ввести исходные данные, распечатать листинг программы, таблицу исходных данных и результатов. При выполнении задания к значениям X1 в четных вариантах 1 прибавляется 1, в нечетных - отнимается 1 . К значениям X2 в 2 четных номерах прибавляется 1.
11. Сделать выводы о применимости метода.
12. Оформить отчет, в котором привести листинг программы, копии экранов и результаты работы программы. Сделать выводы о применимости метода.
Наименование и цель работы; основные положения кратких сведений из теории; индивидуальное задание, в котором привести листинг программы, копии экранов и результаты работы программы. Вывод по работе.
Контрольные вопросы
1. Почему рассмотренный алгоритм называется алгоритмом mвнутригрупповых средних?
2. Докажите,
что для множества точек V={
, 
, …,
) центр кластера Z, обеспечивающий минимизацию суммы квадратов
расстояний до каждой точки из V, представляет собой
выборочное среднее, то есть
.
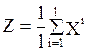3. Примените алгоритм mвнутригрупповых средних к множеству данных, приведенному в задаче 2 из параграфа “Простейший алгоритм выявления кластеров”.
1. Лябах Н.Н. “Математические основы разработки и использования машинного интеллекта” Р-Д , 991 г.,
2. Коршунов Ю.М. “ Математические основы кибернетики”, М, 1987г.
3. . Змитрович А.И. Интеллектуальные информационные системы. «Тэтрасистэм», Минск, 1997г.
4. А. Фор Восприятие и распознавание образов М. «Машиностроение», 1980 г.
Содержание
Введение....................................................................................................................... 4
Лабораторная работа № 1 Методы алгоритмического задания решающих функций. 5
Лабораторная работа № 2.Метод эталона............................................................. 9
Лабораторная работа № 3 Адаптивные методы распознавания.......................... 16
Лабораторная работа № 4 Метод автоматической классификации.................... 18
Лабораторная работа №.5 Простейший алгоритм выявления классов.............. 21
Лабораторная работа № 6 Метод объединения................................................... 24
Лабораторная работа № 7 Алгоритм m внутригрупповых средних................... 26
Список литературы.................................................................................................... 29
Учебное пособие
Наталья Васильевна РЯЗАНЦЕВА
КЛАССИФИКАЦИЯ ОБЪЕКТОВ С ИСПОЛЬЗОВАНИЕМ ТЕОРИИ РАСПОЗНАВАНИЯ ОБРАЗОВ
Методические указания для самостоятельных занятий
по подготовке к лабораторным работам
Редактор…………………………………………
Технический редактор………………………….
Корректор……………………………………….
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.