Классификация объектов с использованием теории распознавания образов: Методические указания для самостоятельных занятий по подготовке к лабораторным работам по курсу «Техническая кибернетика», страница 7

2.  Для проверки работоспособности программы по своему варианту  (номер в журнале) ввести исходные данные, распечатать листинг программы, таблицу исходных данных и результатов. При выполнении задания к значениям X1 в четных вариантах 1 прибавляется 1, в нечетных - отнимается 1 . К значениям X2 в 2 четных номерах прибавляется 1.

3.  Сделать выводы о применимости метода.

4.  Оформить отчет, в котором привести листинг программы, копии экранов и результаты  работы программы. Сделать выводы о применимости метода.

Содержание отчета

Наименование и цель работы; основные положения кратких сведений из теории; индивидуальное задание, в котором привести листинг программы, копии экранов и результаты  работы программы. Вывод по работе.

Контрольные вопросы

1.  Кратко изложить суть адаптивных методов распознавания. Дать геометрическую интерпретацию.

2.  Определить условия применения, преимущества и недостатки метода.

3.  Как изменяются свойства адаптивного алгоритма построения решающего правила в зависимости от значений  - шага коррекции?

4.  Построить разделяющую границу между классами адаптивным методом, если известно, что (0;5); (1;4); (1;6)V1, а (4;0); (5;1); (7;2)  V2. Определить к какому классу принадлежат объекты (1;4) и (0;0).

Лабораторная работа № 4

Методы автоматической классификации

Цель работы: Изучить метод автоматической классификации, выявить преимущества и недостатки метода. Написать  программу, позволяющая классифицировать объекты данным методом.

1 Краткие сведенья из теории

Задача автоматической классификации заключается в следующем. Имеется  выборка объектов, , …,, каждый из которых характеризуется набором признаков X1, X2, … , Xn. Требуется разбить это множество на m классов таким образом, чтобы объекты, объединяющиеся в один класс, были похожи друг на друга по достаточно большому числу признаков. При этом используют гипотезу  “ компактности ” образов, то есть считают, что степень сходства между собой у объектов, принадлежащих одному классу, должна быть больше, чем у объектов, относящихся к разным классам. Геометрически это означает, что классам объектов в признаковом пространстве соответствуют кластеры – однородные, обособленные скопления точек. Число классов m часто является неизвестным и определяется в ходе решения задачи.

В качестве меры сходства объектов и используется расстояние между точками признакового пространства, соответствующими этим объектам:

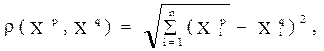при этом, чем меньше расстояние между ними, тем больше сходство.

Алгоритмы выделения кластеров (классов) строятся либо на основе некоторых эвристических соображений ( например, простейший алгоритм выявления кластеров), либо основываются на минимизации (или максимизации) какого-нибудь показателя качества получаемого разбиения объектов на классы (например, алгоритм m внутригрупповых средних).

При эвристическом подходе задается набор правил, которые обеспечивают использование меры сходства для отнесения точек к одному из кластеров. Для установления приемлемой степени сходства двух объектов, объединяемых в один класс, часто вводится некоторый порог T.

Подход, предусматривающий использование показателя качества, связан с разработкой процедур, обеспечивающих минимизацию выбранного показателя качества. Наиболее часто используемым показателем является сумма квадратов отклонений от средних значений

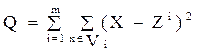, где m– число кластеров;

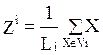    - центр кластера Vi;

L_i - количество объектов, попавших в i –ый кластер.

Очевидно, что чем меньше Q, тем лучше классификация.

Отсутствие априорной информации о значении пороговой величины T меры сходства объектов и числе выделяемых классов m требует проведения многочисленных экспериментов с различными значениями этих параметров для получения приемлемых результатов. Лучшей из полученных при этом классификаций является та, которой соответствует минимальное значение критерия качества Q.