Учебно-методический комплекс дисциплины «Математические основы теории сигналов»

Введение

Целью преподавания дисциплины является изучение общих свойств математического описания сигналов, а также математических методов их исследования, в том числе на ЭВМ.

Дисциплина «Математические основы теории сигналов» является составной частью фундаментальной теоретической подготовки по специальности 5502.

Настоящий курс содержит три раздела:

-  непрерывные сигналы,

-  дискретные сигналы,

-  случайные сигналы.

Успешное овладение курсом «Математические основы теории сигналов» предполагает предварительное изучение студентом курсов «Высшая математика» (разделы «математический анализ», «интегральные преобразования»), «теория вероятностей», «теоретические основы электротехники».

В результате изучения дисциплины студент

должен знать:

1.  основы спектрального анализа сигналов,

2.  особенности описания дискретных сигналов,

3.  основы теории стационарных случайных сигналов;

иметь представление:

1.  о частотно-временной природе сигналов – носителей информации,

2.  о количественных оценках информационных свойств сигналов,

3.  о различных математических моделях представления сигналов.

На основе усвоенных знаний студент должен уметь:

1.  решать задачи спектрального анализа регулярных сигналов, непрерывных и дискретных;

2.  использовать математический аппарат описания моделей динамических систем для построения и анализа систем управления, находящихся под действием регулярных и случайных сигналов.

В соответствии с учебным планом данная дисциплина изучается в 5-м семестре после курса «Математические основы теории систем», изучаемого в 4-м семестре и является естественным продолжением последнего.

Курс «Математические основы теории сигналов» дает теоретические основы для изучения ряда специальных дисциплин, и, в первую очередь, курса «Теория автоматического управления».

Литература

1.  Иванов В.А. и др. Математические основы теории автоматического управления. Т.2. Под ред. проф. Б.К. Чемоданова, М. «Высшая школа», 1977.

2.  Баскаков С.И. Радиотехнические цепи и сигналы. М. «Высшая школа», 1983.

3.  Гутников В.С. Фильтрация измерительных сигналов. Л. «Энергоатомиздат», 1990.

4.  Сиберт У.М. Цепи, сигналы, системы. Т.1, 2. М. «Мир», 1988.

5.  Вентцель Е.С., Овчаров А.А. Теория случайных процессов и ее инженерные изложения. Н. «Наука», 1991.

6.  Вагнер И.Г., Кляуз А.П., Хиценко В.Е. Основы кибернетики. Программа и методические указания для студентов III, IV курса факультета автоматики и вычислительной техники. Новосибирск, 1988.

Программа курса

  I.  Спектральный анализ непрерывных сигналов

Обобщенный ряд Фурье и интеграл Фурье как две формы спектральных представлений непрерывных во времени сигналов.

Задачи спектрального анализа. Спектры и их свойства. Обратимость интеграла Фурье. Симметрия временных и частотных свойств непрерывного сигнала.

Преобразование Лапласа и его свойства.

База сигнала, определение базы. Свойства базы сигнала.

Сигналы ограниченного спектра. Теорема В.А. Котельникова о восстановлении сигнала по его дискретным отсчетам и следствия этой теоремы.

Методические указания

В основе теории сигналов содержится ряд достаточно общих положений, из которых отметим лишь несколько наиболее важных для данного курса.

Математической моделью сигнала  является его представление (разложение) в виде обобщенного ряд Фурье [2, стр. 29]

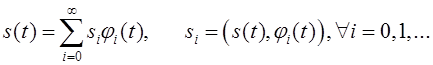                                       (ОРФ)        по ортонормальной системе функций  ( - символ Кронекера), причем коэффициенты такого разложения  определяются как скалярные произведения разлагаемого сигнала на соответствующую базисную функцию , таким образом, для  имеем

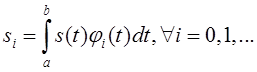                                                                       (КФ)

в соответствии с определением скалярного произведения для пространства .

Формулы (ОРФ) и (КФ) составляют фундаментальный принцип геометрической теории сигналов.

Вторым важным положением теории сигнала является утверждение о двойственной частотно-временной природе сигнала. То есть, для исследования сигнала недостаточно ограничиться лишь его временным представлением . Необходимо также привлечь его частотные (спектральные) характеристики.

Особое значение при этом имеет положение о том, что между частотными и временными свойствами сигнала существует определенная симметрия. Такая симметрия становится еще более полной, если наряду с непрерывным сигналом рассматривать его дискретное представление. Иными словами, симметрия частотных и временных свойств сигнала в полной мере может быть выявлена лишь при рассмотрении этого сигнала в непрерывном и дискретном времени.

И, наконец, указанная симметрия свойств сигналов дополняется аналогичной симметрией свойств непрерывных и дискретных линейных стационарных динамических систем  (ЛСДС). Иными словами, если не ограничиться лишь изучением частотно-временных свойств сигналов, а перейти к более сложной задаче преобразования сигналов ЛСДС, то оказывается, что отмеченная симметрия свойств сигналов дополняется аналогичной симметрией временных и частотных свойств непрерывных и дискретных ЛСДС, преобразующих эти сигналы. Именно это обстоятельство играет существенную роль в описании движения указанных вариантов ЛСДС (непрерывных или дискретных) вызванного тем или иным вариантом сигнального возмущения (непрерывного или дискретного).