Учебно-методический комплекс дисциплины «Математические основы теории сигналов», страница 7

Спектральные характеристики стационарных случайных сигналов и их корреляционных функций.

Эргодические стационарные случайные сигналы.

Прохождение стационарных случайных сигналов через линейные стационарные динамические системы. Основные соотношения.

Среднеквадратичное отклонение в системах автоматического регулирования. Понятие об оптимальном синтезе автоматических систем по минимуму среднеквадратической ошибки.

Методические указания

В основу изложения этого раздела курса вновь положены спектральные представления теперь уже случайных сигналов. Цель такого решения – это желание сохранить единый подход и единую точку зрения на сигналы, имеющие различную природу и различные математические модели.

Принятая частотно-временная концепция изложения теории сигнала заставляет выделять при рассмотрении случайных сигналов те разделы, для которых эта концепция является естественной и наиболее продуктивной. Такими разделами являются «стационарные случайные сигналы (ССС)» и «прохождение ССС через линейные стационарные динамические системы (ЛСДС)». Именно этим разделам уделено в данной части курса основное внимание.

Введем основные понятия и определения. Случайный сигнал  ­­ – это такой сигнал, который в каждый момент времени является случайной величиной. Таким образом, случайные сигналы содержат в себе одновременно черты случайной величины и процесс, протекающий во времени. Именно, случайный сигнал является функцией двух аргументов: времени  ( – область множества значений ) и элементарных событий  ( – пространство элементарных событий), то есть  [5, стр.13].

Таким образом, если зафиксировать один из аргументов случайного сигнала , например время , то этот сигнал вырождается в случайную величину , то есть функцию элементарного события .

Если же зафиксировать второй аргумент, положив , то есть принять, что случайное событие уже произошло и случайный процесс – уже неслучайный, то такой случайный сигнал вырождается в обычную регулярную функцию  аргумента .

Таким образом, случайный сигнал  – это множество (ансамбль) реализаций ,  этого сигнала. Такая вероятностная природа случайного сигнала позволяет для оценки его количественных характеристик оперировать, как и для случайных величин, определенными оценками и характеристиками случайного сигнала.

В качестве таких оценок наиболее широко распространены математическое ожидание , дисперсия  и корреляционная функция  случайного сигнала .

В приложении к случайным сигналам эти оценки являются обобщением соответствующих оценок случайных величин. Так, если известна плотность распределения  случайного сигнала , то его математическое ожидание определено выражением [5, стр.29]

                               ,

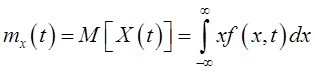где  – оператор математического ожидания,  – возможные непрерывные значения случайной величины, что является обобщением формулы определения математического ожидания

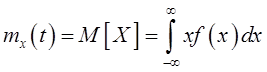
случайной величины .

Аналогичным образом для дисперсии  случайного сигнала  имеем [5, стр.31]

                  .

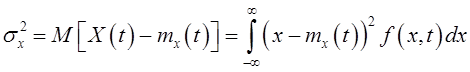Замечаем, что оценки ,  являются неслучайными (регулярными) характеристиками случайного сигнала .

Наряду с оценками ,  – функциями одного аргумента , большое значение для характеристики случайных сигналов имеют корреляционные функции. Для сигнала  корреляционная функция определяется выражением вида [5, стр.33]

                    ,

то есть является функцией двух аргументов , .

Корреляционная функция (КФ) обладает следующими свойствами [5, стр.33-35]:

1.   и ;

2.  , то есть КФ симметрична по , ;

3.  КФ является положительно определенной, то есть , что является обобщением понятия положительной определенности матрицы.

Вычисление корреляционных функций для случайных сигналов общего вида, определение движения линейных динамических систем под действием случайных сигналов, а также корреляционных функций такого движения существенно упрощается, если случайные сигналы представить в виде их канонических разложений. Каноническое разложение (КР) случайного сигнала  имеет вид [5, стр.262-268]