Учебно-методический комплекс дисциплины «Математические основы теории сигналов», страница 2

Среди возможных реализаций ортонормального базиса  (ОРФ) особую роль играют различные варианты ортогонального базиса гармонических функций, какими являются , , , , . Это объясняется тем обстоятельством, что указанные гармонические функции являются собственными функциями операторов ЛСДС и, потому, сохраняются при преобразовании их ЛСДС, изменяясь лишь по амплитуде и фазе. Отсюда следует, что если какой-либо сигнал , представленный своим разложением в виде ряда Фурье [2, стр.38-39]

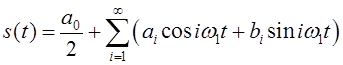                            ,                            (РФ)

где , ,  - коэффициенты разложения, преобразован ЛСДС, то базисные функции  такого разложения сохраняются при таком преобразовании с точностью до амплитуды и фазы. Эта неизменность базиса на выходе ЛСДС сводит определение выходного сигнала такой системы лишь к пересчету коэффициентов ,  разложения (РФ).

Наиболее распространенным вариантом гармонического ряда Фурье разложения сигналов является экспоненциальный (комплексный) ряд Фурье вида [2, стр.42-48]

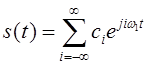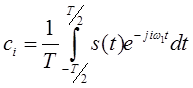                           , .                         (КРФ)

Широкое применение этого варианта ряда Фурье объясняется тем обстоятельством, что базис (КРФ), то есть набор функций , сохраняется при многократном дифференцировании, в то время как в разложении (РФ) косинусы переходят в синусы и наоборот. При этом существует связь между коэффициентами разложения рядов (РФ) и (КРФ) в виде

                                     ,

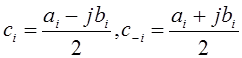откуда следует, что , , .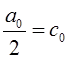

Дадим теперь разъяснение таких важных понятий как спектр и спектральная характеристика. Именно, спектром сигнала является совокупность всех коэффициентов Фурье любого из разложений (ОРФ), (РФ), (КРФ) сигнала . То есть, для ряда (ОРФ) спектром являются коэффициенты , , для ряда (РФ) ­­­­- это пары , , для ряда (КРФ) – это, соответственно, совокупность комплексных чисел , . При этом, для гармонического ряда Фурье выделяют амплитудный спектр, каким является набор положительных чисел (амплитуд гармоник)

                           , ,

для рядов (РФ) и (КРФ) соответственно, и фазовый спектр, определяемый значением углов (фаз гармоник)

                           , ,

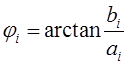соответственно.

Имеет место утверждение, что спектр полностью определяет сигнал. И главное в этом утверждении не только тот факт, что знание коэффициентов Фурье какого-либо сигнала дает возможность с помощью соответствующего ряда Фурье восстановить этот сигнал. Здесь речь идет о возможности анализа любого сигнала с помощью его спектра. Действительно, любой ряд Фурье является своеобразным фильтром, который выявляет состав гармоник, содержащихся в этом сигнале, причем коэффициенты Фурье (спектр) определяют «вес» каждой из этих гармоник. Важной также является скорость убывания спектральных составляющих сигнала, что напрямую определяет точность аппроксимации сигнала его конечной суммой, например [2, стр.32-33]

                                            .                                             ()

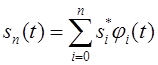При этом оказывается, что имеет место так называемое оптимальное свойство коэффициентов Фурье , , заключающееся в том, что, если в частичной сумме () коэффициенты ,  выбраны в соответствии с формулой (КФ), то среднеквадратичное отклонение сигнала  от его аппроксимации , то есть величина , будет минимальной для любых сигналов  для всех ортонормальных базисов  и для всех чисел  в формуле ().

Итак, введение ряда Фурье для какого-либо сигнала  дает возможность дополнительно привлечь к исследованию этого сигнала развитый аппарат ортогональных рядов.

Однако, наряду с изучением свойств сигналов важным является изучение прохождения сигналов через ЛСДС. С этой целью в рассмотрение вводится также Фурье-преобразование сигнала , то есть интеграл вида

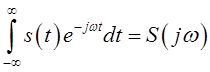                                       ,                                          (F)

где функция частоты , то есть  называется спектральной плотностью сигнала .