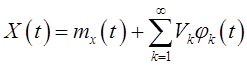 , (КР)
, (КР)
где ![]() –
некоррелированные случайные величины с нулевыми средними,
–
некоррелированные случайные величины с нулевыми средними, ![]() – неслучайные линейно независимые функции
аргумента
– неслучайные линейно независимые функции
аргумента ![]() ,
, ![]() –
математическое ожидание сигнала
–
математическое ожидание сигнала ![]() .
.
Из разложения (КР) следует, что каноническое разложение
сигнала ![]() есть, по сути, обобщение ряда Фурье на
область случайных сигналов, где некоррелированные случайные величины
есть, по сути, обобщение ряда Фурье на
область случайных сигналов, где некоррелированные случайные величины ![]() ,
, ![]() и
функции
и
функции ![]() ,
, ![]() играют
роль базисов в пространствах случайных событий и регулярного переменного
играют
роль базисов в пространствах случайных событий и регулярного переменного ![]() соответственно.
соответственно.
При этом в отношении случайного сигнала ![]() имеют место следующие результаты:
имеют место следующие результаты:
1.
Корреляционная функция ![]() сигнала
сигнала ![]() имеет вид [5, стр.266]
имеет вид [5, стр.266]
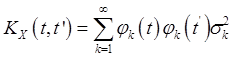 , (КРКФ)
, (КРКФ)
где ![]() –
дисперсии случайных величин
–
дисперсии случайных величин ![]() . При этом говорят, что
каноническое разложение (КР) сигнала
. При этом говорят, что
каноническое разложение (КР) сигнала ![]() соответствует
каноническому разложению
соответствует
каноническому разложению ![]() его корреляционной
функции.
его корреляционной
функции.
Имеет место и обратное утверждение, то есть, если КФ
какого-либо сигнала ![]() представима в виде (КРКФ), то
центрированный случайный сигнал
представима в виде (КРКФ), то
центрированный случайный сигнал ![]() имеет вид (КР), то есть
имеет вид (КР), то есть
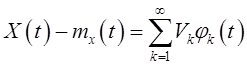 ,
,
где случайные величины ![]() имеют своими дисперсиями числа
имеют своими дисперсиями числа ![]() из разложения (КРКФ).
из разложения (КРКФ).
2.
Если случайный сигнал ![]() , представленный своим
разложением (КР), преобразуется линейной динамической системой с оператором
, представленный своим
разложением (КР), преобразуется линейной динамической системой с оператором ![]() в сигнал
в сигнал ![]() , то
есть имеет место преобразование
, то
есть имеет место преобразование
![]() ,
,
то для сигнала ![]() также получаем каноническое разложение [5,
стр.282-283]
также получаем каноническое разложение [5,
стр.282-283]
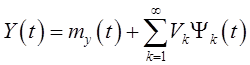 , (КР)
, (КР)
где ![]() ,
, ![]() ,
, ![]() Откуда следует,
что преобразованию
Откуда следует,
что преобразованию ![]() подвергается лишь регулярные
составляющие сигнала
подвергается лишь регулярные
составляющие сигнала ![]() . Очевидно также, что
корреляционная функция сигнала
. Очевидно также, что
корреляционная функция сигнала ![]() имеет вид
имеет вид
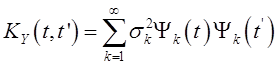 . (КРКФ)
. (КРКФ)
Дальнейшее существенное упрощение в определении
преобразований случайного сигнала ![]() и оценок таких
преобразований имеет место для частного случая сигналов
и оценок таких
преобразований имеет место для частного случая сигналов ![]() ,
которые являются стационарными случайными сигналами. Рассматривается
стационарность в широком смысле, когда для сигнала
,
которые являются стационарными случайными сигналами. Рассматривается
стационарность в широком смысле, когда для сигнала ![]() выполняются
следующие условия [5, стр.306-307]:
выполняются
следующие условия [5, стр.306-307]:
![]() ,
, ![]() ,
, ![]() ,
,
причем главным условием является
зависимость корреляционной функции такого процесса от разности аргументов ![]() , то есть фактически от одного аргумента
, то есть фактически от одного аргумента ![]() .
.
В этом случае, приняв каноническое разложение сигнала ![]() в виде [5, стр.331-335]
в виде [5, стр.331-335]
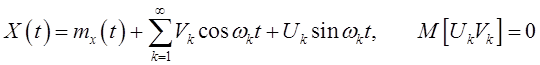
получаем (КРКФ) такого сигнала ![]() в виде
в виде
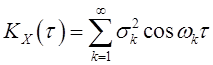 , (
, (![]() )
)
причем дисперсии ![]() случайных величин
случайных величин ![]() ,
,
![]() , то есть
, то есть ![]() ,
оказываются коэффициентами Фурье в разложении корреляционной функции
,
оказываются коэффициентами Фурье в разложении корреляционной функции ![]() . Таким образом, получаем [5, стр.333]
. Таким образом, получаем [5, стр.333]
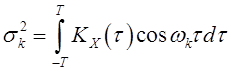
![]() .
.
Отсюда непосредственно следует, что, зная корреляционную
функцию ![]() какого-либо стационарного сигнала
какого-либо стационарного сигнала ![]() , можем получить дисперсии
, можем получить дисперсии ![]() случайных величин
случайных величин ![]() ,
,
![]() его канонического разложения. Более того,
из равенства
его канонического разложения. Более того,
из равенства ![]() и формулы (
и формулы (![]() ) следует [5, стр.333]
) следует [5, стр.333]
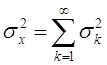 ,
,
то есть дисперсия сигнала ![]() равна сумме дисперсий составляющих его
гармоник.
равна сумме дисперсий составляющих его
гармоник.
Наряду с аналогом ряда Фурье регулярных сигналов для
стационарных случайных сигналов с помощью преобразования Фурье вводится аппарат
спектральных плотностей. Так, для корреляционной функции ![]() сигнала
сигнала ![]() введением
спектральной плотности [5, стр.335-337]
введением
спектральной плотности [5, стр.335-337]
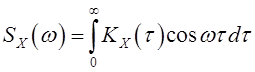
получают пару функций частоты – ![]() и времени –
и времени – ![]()
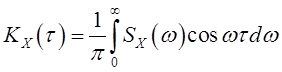 ,
,
представляющих собой прямое и обратное косинус-Фурье преобразование. Таким образом, наряду с рядами Фурье, введение непрерывных спектральных преобразований создает основу спектрального анализа стационарных случайных сигналов, аналогичную спектральному анализу регулярных сигналов.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.