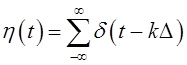Учебно-методический комплекс дисциплины «Математические основы теории сигналов», страница 5

                                         ,

то есть на интервале  времени, причем  - шаг квантования.

Отметим, что операция произведения трактуется различно при определении двух указанных моделей дискретизации. В одном случае непрерывный сигнал  при умножении на функцию  преобразуется в соответствии с выражением

                       .

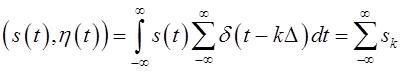При этом полагают, что 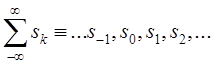, что приводит к решетчатой функции, определяемой последовательностью ее дискретных значений , соответствующих значениям аргумента . Описанный таким образом процесс дискретизации непрерывного сигнала используется при рассмотрении процессов во временной области.

При рассмотрении дискретных сигналов в частотной области используется вторая модель дискретизации, при которой произведение непрерывного сигнала  и функции  определено в виде [2, стр.376-377]

                   .

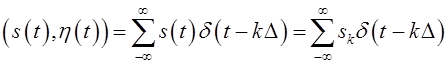Отсюда окончательно следует

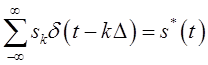
определение модулированной импульсной последовательности , то есть последовательности дискретных значений , умноженных на соответствующие по времени  - функции . Такие функции  называются МИП сигналов .

Если теперь вычислить спектральную плотность такой МИП , то есть вычислить Фурье-преобразование , то получим [2, стр.378]

                                 .                                  ()

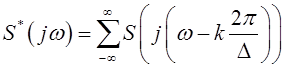Формула () устанавливает, что спектральная плотность  МИП

-  во первых, представляет собой бесконечную сумму «копий» спектральной плотности  исходного непрерывного сигнала , смещенных в области частот на интервалы 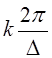, где ;

-  во вторых,  является непрерывной периодической функцией частоты  с периодом .

Это дает возможность сделать вывод о существовании еще одной симметрии временных и частотных свойств теперь уже в непрерывных и дискретных сигналах. Именно, непрерывные и периодические во времени сигналы  имеют дискретный непериодический спектр (коэффициенты Фурье , ), а дискретные непериодические во времени сигналы  имеют непрерывный периодический спектр  в частотной области.

Для дискретных сигналов  существуют обобщения основных представлений непрерывного сигнала в виде дискретного ряда Фурье (ДРФ), дискретного преобразования Фурье (ДПФ), дискретного преобразования Лапласа (ДПЛ) и тому подобные.

Совокупность этих дискретных представлений и преобразований дискретных сигналов  играет ту же роль в дискретном времени, что и одноименные представления и преобразования в непрерывном времени для непрерывных сигналов. Так, преобразование Фурье () для МИП, выраженное через ее дискретные выборки  и их множители , то есть [4(2), стр.280-281]

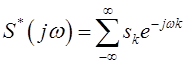                                                                                 (ДРФ)

называется дискретным рядом Фурье (ДРФ). Таким образом, (ДРФ) устанавливает частотные свойства МИП , как и выражение (), но используя отсчеты  временного представления .

Если провести инверсию ДРФ, то можно восстановить значения оригиналов , , то есть решетчатую функцию по дискретной спектральной плотности . Причем, учитывая периодичность последней, нужная формула вычисления отсчетов  примет вид

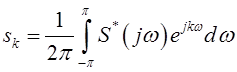                         , .                   (ОДРФ)

Для пары дискретных преобразований (ДРФ) и его обращения (ОДРФ) справедливы основные положения спектрального анализа непрерывных сигналов. Именно, (ДРФ) и (ОДРФ) могут быть представлены в синусной и косинусной формах. Для ДРФ могут быть введены амплитудные и фазовые частотные характеристики и тому подобные.

Теперь перейдем к рассмотрению дискретных периодических последовательностей  с числом выборок  на периоде  дискретного времени, так что , где  – шаг квантования по времени. Очевидно, что совокупность этих дискретных значений , , может быть истолкована как вещественный -мерный вектор . Для этого вектора  в  можно ввести невырожденное преобразование , отображающее его в -мерное комплексное пространство , так что получаем пару преобразований , , определяемых соотношениями вида [2, стр.380-384; 4(2), стр.280]