Учебно-методический комплекс дисциплины «Математические основы теории сигналов», страница 6

                                           ,                                        (ДПФ)

                                            .                                     (ОДПФ)

При этом отображение  вещественного -мерного вектора  в комплексный-мерный вектор  называется дискретным преобразованием Фурье, а обратное к нему преобразование  – обратное дискретное преобразование Фурье (ОДПФ), оно задается выражением (ОДПФ) и соотношением

                                               .

В отношении преобразований ДПФ и ОДПФ и векторов ,  отметим следующие положения.

1.  Компоненты ,  векторов , , в силу соотношений (ДПФ), (ОДПФ) выражаются в виде

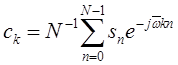
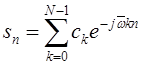
                               ,                           (ДПФ)

                                  ,                           (ОДПФ)

где  – относительная частота.

2.  Преобразование ДПФ также порождает периодическую дискретную последовательность  комплексных чисел.

Таким образом, взаимообратные преобразования  и  отображают дискретную периодическую вещественную последовательность  в дискретную периодическую комплексную последовательность  и обратно.

3.  Конечномерные операторы  и  порождены ортогональными решетчатыми функциями  двух дискретных аргументов: времени () и частоты (), заданных на  отсчетах - периодической функции времени и частоты.

4.  Конечномерный комплекснозначный оператор  своими столбцами задает ортогональный базис [2, стр. 384-386]

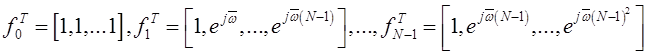
называемый базисом Фурье, так что , причем . Таким образом, (ОДПФ) вида  может быть истолковано как разложение вектора  по базису Фурье . В этом случае коэффициенты такого разложения определяются по формуле . Непосредственное сравнение этого выражения с определением коэффициента  в (ДПФ) показывает их полное совпадение. Отсюда можно сделать вывод о том, что ДПФ действительно есть разложение вектора  временной последовательности по базису Фурье. Таким образом, получаем возможность ввести в спектральный анализ ДПФ и ОДПФ, наряду с аналитическим, аппарат линейной алгебры.

ДПФ имеет широкое применение в теории и практике дискретных сигналов. Его использование в этой области аналогично применению преобразования Фурье для непрерывных сигналов.

Особое значение здесь приобретают различные схемы быстрого дискретного преобразования Фурье (БПФ), являющиеся развитием ДПФ [2, стр.385-387;3, стр.65-67].

В заключение этого раздела приведем еще одну таблицу, которая иллюстрирует дополнительные симметричные связи, имеющие место между различными областями непрерывных и дискретных сигналов и их частотных представлений.

Таблица 2

Из табл.2 легко видеть, что введение ограничений периодичности и дискретности на сигналы во временной области симметрично отражается на их спектральных характеристиках. При этом необходимо отметить, что табл.1, иллюстрирующая симметрию временных и частотных свойств непрерывных сигналов, относиться лишь к первой строчке табл.2.

  III.  Случайные сигналы

Понятия о случайных сигналах (функциях). Математическое ожидание, дисперсия и корреляционная функция ­­­­­­­­­­­­– основные оценки случайных сигналов.

Канонические разложения случайных сигналов.

Стационарные случайные сигналы. Стационарность случайных сигналов по математическому ожиданию дисперсии и корреляционной функции.