Учебно-методический комплекс дисциплины «Математические основы теории сигналов», страница 3

При этом совершенно очевидно различие между рядом Фурье (РФ) и интегралом (F). Именно, ряд Фурье есть разложение (представление) сигнала : он содержит те составляющие  сигнала , которые присутствуют (находятся) в этом сигнале, причем, доля каждой базисной функции  определена весовыми коэффициентами . Иное дело интеграл (F), который задает преобразование сигнала , отображая его из пространства сигналов – функций времени  в пространство сигналов – функций частоты . Более того, функция  имеет смысл спектральной плотности, поскольку можно показать, что значения этой функции на частотах , то есть , определяются выражением [2, стр.44; 5, стр.336]

                                          .

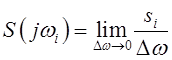Таким образом, спектральная характеристика описывает плотность коэффициентов Фурье  по частоте , то есть имеет смысл производной по частоте.

С введением преобразования (F) в теорию сигнала дополнительно вводятся, наряду с представлением функций-оригиналов, описывающих сигналы  во временной области, также функции-изображения , описывающие эти же сигналы как функции мнимой частоты . Данное обстоятельство позволяет использовать для анализа этих функций развитый аппарат теории функций комплексного переменного.

Важным является также тот факт, что, наряду с отображением функций-оригиналов  в пространство их отображений, существует также возможность отображения в это пространство различных преобразований сигналов  в соответствующие преобразования их изображений. Таким образом, наряду с пространством сигналов  и их преобразований во временной области, существует пространств изображений этих сигналов  с соответствующими преобразованиями в частотной области [3, стр.11-15].

Существование такой пары пространств и операций в них является теоретической основой спектрального анализа, в котором совместно используются элементы обоих пространств и их преобразования.

При этом имеет место замечательная симметрия временных и частотных представлений сигналов и их преобразований в обоих пространствах. Здесь укажем лишь небольшую часть такой симметрии (табл.1).

Таблица 1

Студентам предлагается привести дополнительные примеры указанной симметрии, «развивая» табл.1.

Принципиально важным следствием отмеченной симметрии является обратимость пары Фурье-преобразований () и (). Здесь речь идет не о существовании прямого () и обратного () преобразования Фурье, согласно которым, если

                ,

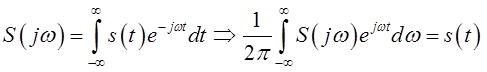так что

                                  [3, стр.15-16].

Под обратимостью преобразований Фурье понимают тот факт, что  обратимо с точностью до знака аргумента. То есть, если для какого-либо оригинала  имеем связь , то отсюда следует, что  и .

Обратимость преобразований Фурье особенно показательна, если такому преобразованию подвергаются вещественные четные сигналы, то есть такие, что . Тогда их изображения – также четные и вещественные функции частоты, то есть , и, более того, если , то  [2, стр.114; 3, стр.15-18].

Наряду с преобразованием Фурье вида () широко используется также преобразование Лапласа сигнала  [2, стр.61-65]

                                , .                                 ()

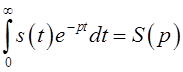Как видим, обобщение преобразования Фурье здесь достигается переходом от мнимой частоты  интеграла Фурье к комплексному аргументу  преобразования Лапласа. Такой переход позволяет:

-  во первых, ввести частотные представления для сигналов, не преобразуемых по Фурье;

-  во вторых, провести алгебраизацию задачи прохождения сигналов через линейные стационарные динамические системы, в случае, когда эти системы описываются сверткой либо линейными дифференциальными уравнениями с постоянными коэффициентами.

Особую роль в теории сигнала имеет понятие базы сигнала, то есть произведение его важнейших характеристик – эффективной длительности сигнала  и полосы его существенных частот . То есть для базы сигнала имеем [4(1), стр.193-204]