Дискретные системы автоматического управления, страница 13

где  - частота среза спектра .

Финитным называется спектр сигнала, для которого выполняется условие (5.24). Пример сигнала с финитным спектром показан на рис. 5.19. Там же показаны спектры дискретизированного финитного сигнала при различных частотах дискретизации. Из рисунка видно, что при , имеется наложение спектральных слагаемых и, следовательно, выделение исходного спектра  из спектра дискретного сигнала  невозможно. При  наложения нет, а, следовательно, пропустив дискретный сигнал через идеальный фильтр нижних частот (ФНЧ) с коэффициентом передачи в полосе пропускания, равным  и частотой среза , можно выделить спектр , что означает полное восстановление дискретизируемого сигнала . Частота    (или ), которая ограничивает сверху диапазон

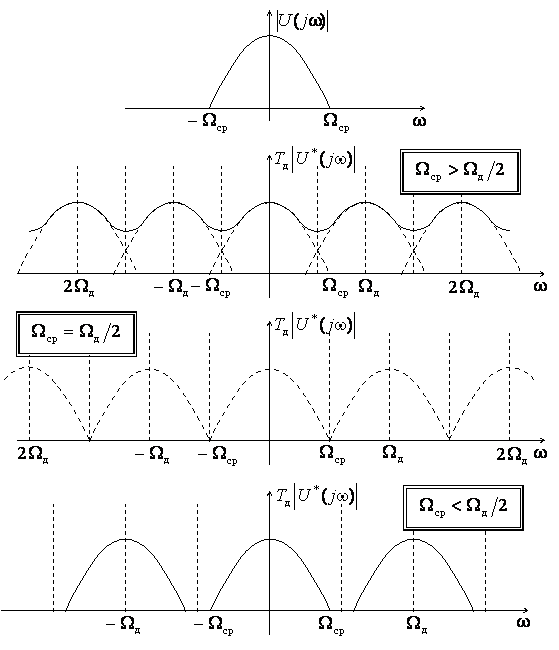
Рис. 5.19. Спектр непрерывного финитного сигнала и масштабированный спектр дискретизированного сигнала при различных частотах дискретизации

частот, в котором возможно квантование без потерь информации, называется частотой Найквиста.

Характеристика восстанавливающего ФНЧ показаны на рис. 5.20.

Рис. 5.20. АЧХ идеального восстанавливающего ФНЧ

С указанным выше фактом связано содержание теоремы Котельникова: аналоговый сигнал  с финитным спектром, ограниченным частотой , может быть без потерь информации представлен отсчетами, взятыми с частотой дискретизации , если выполняется условие: