3 Симплекс-метод решения задачи линейного программирования. 49
3.1 Векторная запись задачи линейного программирования. Опорный план. 50
3.2 Сущность симплекс-метода. 52
3.2.1 Пример решения задачи линейного программирования симплекс-методом.. 54
3.2.2 Решение задачи в общем виде. Симплексная таблица. 58
3.3 Решение задачи производственного планирования симплекс-методом.. 68
3.4 Вопросы и упражнения. 70
Графический способ решения задачи линейного программирования целесообразно использовать для задач небольшой размерности (с двумя переменными) или задач, которые могут быть сведены к задачам с двумя переменными. Можно строить и трехмерные графики, хотя это уже несколько сложнее. Достоинствами этого метода являются его простота и наглядность. Однако на практике при построении экономико-математических моделей обычно вводится большее количество переменных, что делает необходимым использование более сложных методов.
Симплекс-метод представляет собой общий аналитический метод решения задачи линейного программирования*.
Так же, как и при использовании графического способа решения, идея симплекс-метода состоит в рассмотрении вершин области допустимых планов (ОДП) в многомерном пространстве и в определении на основании некоторого критерия, является ли рассматриваемый план оптимальным.
При этом симплекс-метод предлагает алгоритм такого направленного перебора этих вершин, при котором нет необходимости рассматривать их все, поскольку при переходе от одного плана к другому происходит приближение к искомому решению (или установление неразрешимости).
Однако, если при использовании графического метода вершины ОДП можно было определить визуально, то в симплекс-методе это уже можно сделать только аналитически. Поэтому для описания алгоритма рассматриваемого метода необходимо ввести некоторые понятия.
Система ограничений задачи линейного программирования, приведенной к канонической или стандартной форме, может быть записана в векторной форме следующим образом:
![]()
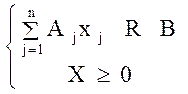 ,
,
где Аj = 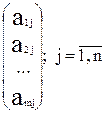 - векторные коэффициенты; B=
- векторные коэффициенты; B=![]() , X=
, X=![]() , R Î
{£;³;=}.
, R Î
{£;³;=}.
Будем считать, что система ограничений задачи в канонической форме представляет собой линейно независимую систему уравнений (в противном случае часть уравнений можно просто вычеркнуть).
Опорным планом задачи линейного программирования в канонической форме называется такой допустимый план, совокупность векторных коэффициентов при ненулевых компонентах которого представляет собой систему линейно независимых векторов*.
![]() Например, представим
систему ограничений задачи, записанной в канонической форме, в векторной форме:
Например, представим
систему ограничений задачи, записанной в канонической форме, в векторной форме:
2х1 + 3х2 - х3 + х4 = 5
4х1 + 6х2 + 2х3 + х5 = 10
х1-5 ³ 0
А1 = ![]() , А2
=
, А2
= ![]() , А3 =
, А3 = ![]() ,
А4 =
,
А4 = ![]() , А5 =
, А5 = ![]() , В =
, В = ![]() , Х =
, Х = ![]() ;
;
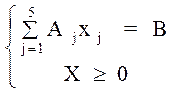 .
.
Рассмотрим план Х(1) = (0; 0; 0; 5; 10). Этот план является допустимым, в чем легко убедиться, подставив его в систему ограничений:
![]() 2*0
+ 3*0 - 0 + 5 = 5
2*0
+ 3*0 - 0 + 5 = 5
4*0 + 6*0 + 2*0 + 10 = 10
0 ³ 0
5 ³ 0
10 ³ 0
Отличными от нуля являются переменные х4 и
х5. Векторные коэффициенты при этих переменных А4 = ![]() и А5 =
и А5 = ![]() являются
линейно независимыми. В самом деле,
являются
линейно независимыми. В самом деле, 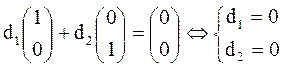 . Следовательно, план Х(1)
является опорным.
. Следовательно, план Х(1)
является опорным.
Убедимся в том, что отнюдь не любой допустимый план является опорным. Для этого рассмотрим другой план Х(2) = (1; 1; 0; 0; 0). Здесь ненулевыми компонентами плана являются переменные х1 и х2. Этот план тоже является допустимым:
2*1 + 3*1 - 0 + 0 = 5
![]() 4*1
+ 6*1 + 2*0 + 0 = 10
4*1
+ 6*1 + 2*0 + 0 = 10
1 ³ 0
0 ³ 0
Однако этот план не является опорным, так как можно
подобрать отличные от нуля числа d1 и d2, при которых d1А1+
d2А2 = d1![]() +d2
+d2![]() =
= ![]() . Таких
чисел бесконечно много, например, d1 = 3, d2 = -2.
. Таких
чисел бесконечно много, например, d1 = 3, d2 = -2.
Можно доказать [6], что каждой вершине ОДП задачи линейного программирования соответствует опорный план. Поэтому, чтобы найти оптимальный план в одной из вершин, симплекс-метод перебирает именно опорные планы задачи линейного программирования.
Очевидно, что ненулевых компонент в опорном плане может быть не больше, чем ограничений в задаче (в рассмотренном примере невозможно построить три двумерных линейно независимых вектора, поэтому ненулевых компонент не может быть больше двух). Для реализации симплекс-метода необходимо, чтобы в опорном плане присутствовало ровно m линейно независимых векторов, т.е. базис m–мерного пространства. В случае, если ненулевых компонент в опорном плане меньше, чем m, один или несколько из этих векторов могут соответствовать и нулевым переменным. Переменные, столбцы коэффициентов при которых образуют полную систему (m) единичных независимых столбцов, будем называть базисными (хБ), а остальные переменные - небазисными. Столбцы (вектора), соответствующие базисным переменным, также будем называть базисными. Совокупность этих переменных (или этих векторов) будем называть базисом. Если среди базисных переменных есть нулевые, базис называют вырожденным.
Например, в плане Х(1) в базис входили переменные х4 и х5, и базис был невырожденным.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.