Симплекс-метод может быть применен для решения любой задачи линейного программирования, однако в общем случае приходится использовать различные его модификации. Рассмотрим вначале его применение для задачи линейного программирования, удовлетворяющей следующим условиям:
а) на все переменные наложены ограничения неотрицательности, а все остальные ограничения (пусть их m) представляют собой уравнения;
б) свободные члены ограничений неотрицательны;
в) среди векторных коэффициентов имеется полный набор линейно независимых векторов, который представляет собой m единичных столбцов.
Отметим, что задача, удовлетворяющая первому условию, представляет собой задачу линейного программирования в канонической форме. Любая задача линейного программирования в смешанной форме (т.е. в общем виде) может быть к ней приведена (см. раздел 1.4.1).
Что касается двух других условий, то в ряде частных случаев (но отнюдь не всегда) можно добиться их выполнения, умножив или разделив обе части ограничения на одно и то же число. Так, если свободный член в ограничении отрицателен, можно умножить обе части уравнения на -1. Если после этого одного из единичных векторов не хватает, но в соответствующем ограничении присутствует с некоторым положительным коэффициентом переменная, которая в другие ограничения не входит, то обе части этого ограничения можно разделить на данный коэффициент. Например, если одно из ограничений имеет вид -4х1 - 6х2 + 2х3 - 2х4 = -10, и, например, переменная х4 в других ограничениях не встречается, то разделив обе части на -2, можно получить 2х1 + 3х2 - х3 + х4 = 5. В полученном уравнении свободный член неотрицателен, и векторный коэффициент при х4 является единичным.
Задачу, удовлетворяющую перечисленным условиям, можно записать в общем виде следующим образом (для задачи на максимум):
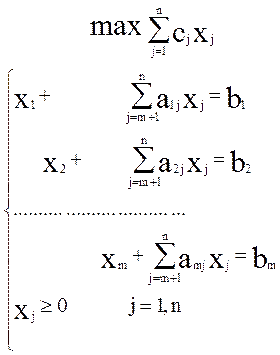
Разумеется, единичные вектора не обязательно должны стоять при первых m переменных. Однако переменные всегда можно обозначить по-другому, перенумеровать, поэтому запись (14) все-таки можно считать общей.
Опорный план построим
следующим образом: базисные переменные (в (14) это первые m переменных) примем
равными соответствующим элементам столбца свободных членов, а небазисные - равными
нулю. Таким образом, исходный опорный план Х = (b1, b2, .
. . bm, 
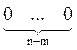). Такой план, очевидно, является
допустимым, что легко проверить, подставив его в систему ограничений:
b1 + 0 = b1
b2 + 0 = b2
…
bm + 0 = bm
b1-m ³ 0; 0 ³ 0
Векторные коэффициенты при его ненулевых компонентах b1-m представляют собой линейно независимые единичные столбцы; т.е. этот план действительно опорный. Далее применение симплекс-метода рассмотрим на примере.
Решим следующую задачу:
max -5х1 + 2х3
-5х1
- х2 + 2х3 £ 2
-х1 + х3 + х4 £ 5
-3х1 + 5х4 £ 7
х1-4 ³ 0
Приведем ее к канонической форме.
max -5х1 + 2х3
-5х1 - х2 + 2х3 + х5 = 2
-х1 + х3 + х4 + х6 = 5
-3х1 + 5х4 + х7 = 7
х1-7 ³ 0
Теперь пример имеет вид задачи (14) с той разницей, что единичные вектора стоят не при первых трех, а при последних трех переменных - х5, х6 и х7; но изменять обозначения не имеет смысла.
Для удобства дальнейших рассуждений ограничения пронумеруем. При этом обозначим значение целевой функции (-5х1 + 2х3) = z и припишем к системе новое (четвертое) ограничение, после чего задача примет следующий вид:
max z
1) -5х1 - х2 + 2х3 + х5 = 2
2) -х1
+ х3 + х4 + х6 = 5
3) -3х1 + 5х4 + х7 = 7
4) z + 5х1 - 2х3 = 0
х1-7 ³ 0
Решений такой системы бесконечно много.
При последних трех переменных (дополнительных) стоят
единичные столбцы: А5 = 
, А6 = 
и А7 = 
.
Поэтому удобно взять переменные х5, х6 и х7 в
качестве базисных. Приравняем их к свободным членам, а остальные – к нулю.
Таким образом мы получим исходный опорный план - одно из решений этой системы -
Хо =
= (0; 0; 0; 0; 2; 5; 7).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.