Симплекс-метод решения задачи линейного программирования, страница 5

Чтобы избежать этого, выразим базисную переменную х₃ из первого ограничения через небазисные (-2,5х₁ – 0,5х₂ + х₃ + 0,5х₅ = 1 Û х₃ = 1 +
+ 2,5х₁ + 0,5х₂ - 0,5х₅) и подставим в целевую функцию: z = -5х₁ + 2х₃ = -5х₁ +
+ 2*(1 + 2,5х₁ + 0,5х₂ - 0,5х₅) = 2 + х₂ - х₅. Теперь уравнение z - 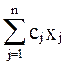 = 0 примет вид: z + х₂ - х₅ = 2, т.е. вид уравнения (4`) из системы (16). Рекомендуется сравнить остальные ограничения последней задачи с уравнениями (16): они в точности совпадают; и целевая функция взята из того же примера.

Итак, в общем случае после введения критериального ограничения столбцы при базисных переменных могут перестать быть единичными. Чтобы избежать этого, выразим базисные переменные x_1-m из ограничений через небазисные:

x₁ = b₁ - a_{1 m+1}x_m+1 - . . . -a_{1 n}x_n

…

x _i = b _i - a _{i m+ 1}x_{m+ 1} - . . . -a _{i n}x_n

…

x_m = b_m - a_{m m+1}x_m+1 - . . . -a_{m n}x_n

и подставим их в целевую функцию: z = 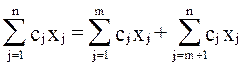 = c₁(b₁ -
- a_{1 m+1}x_m+1 - . . . -a_{1 n}x_n) + . . . + c_m(b_m - a_{m m+1}x_m+1 - . . . - a_{m n}x_n) + c_m+1x _m+1 + . . . +
+ c_nx_n.

После приведения подобных членов и переноса свободного члена в правую часть критериальное ограничение примет следующий вид: z + x_m+1(c₁a_{1 m+1} + . . . + c_ma_{m m+1} - c _m+1) + . . . + x_n(c₁a_{1 n}+ . . . + c_ma_{m n} - c_n) = c₁b₁ +
+ . . . + c_mb_m; или x_m+1(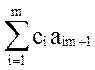 - c_m+1) + … + x_n( 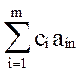- c_n) = .

Обозначим коэффициенты при переменных x_j в критериальном ограничении - D_j =  - c_j; а свободный член этого ограничения - d = .

Отметим, что коэффициенты при базисных переменных в критериальном ограничении будут нулевыми, что и требовалось получить. Но и эти нулевые коэффициенты также можно рассчитать по формулам ( - c_j): поскольку базисные переменные входят лишь в одно ограничение, в этих формулах только одно слагаемое в сумме  слева будет ненулевым. Для  базисных переменных .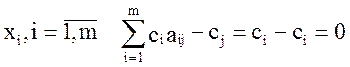

Таким образом, критериальное ограничение примет вид:

z + 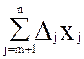 = d

Теперь исходные данные задачи линейного программирования можно записать в виде симплексной таблицы (таблица 7).

Каждая строка таблицы соответствует одному ограничению задачи линейного программирования ((m+1)-я строка - критериальному ограничению).

Левая часть таблицы (первые три столбца) является вспомогательной - в ней в первом столбце указывается номер строки, во втором (x_б) - базисная переменная, соответствующая каждой строке (та, которая входит в это ограничение с коэффициентом 1), в третьем (с_б)  - коэффициент целевой функции при соответствующей базисной переменной.

В правой части таблицы в столбце В указаны свободные члены системы ограничений (в (m+1)-ой строке - значение целевой функции на опорном плане d), а все остальные столбцы соответствуют переменным задачи линейного программирования, и в них указаны коэффициенты при этих переменных в каждом ограничении.

Над обозначениями переменных в верхней части таблицы рекомендуется указывать соответствующие коэффициенты целевой функции.

Таблица 7 – Симплексная таблица