Симплекс-метод решения задачи линейного программирования, страница 7

Левая (вспомогательная) часть новой таблицы будет отличаться только содержанием t-й строки столбцов х_б и с_б: вместо х_t и с_t там будет стоять соответственно х_к и с_к, так как переменная х_t из базиса выйдет, а х_к войдет.

Правая часть таблицы подвергнется преобразованию методом Гаусса. Цель преобразования - получить единичный столбец при переменной х_к, причем единица должна будет стоять на месте разрешающего элемента, т.е. в t-ой строке. Общие формулы для таких преобразований выглядят следующим образом (со штрихом обозначены элементы новой таблицы):

а_tj`= а_tj / а_tk ;

b_t`= b_t / а_tk – вся разрешающая строка делится на разрешающий элемент, при этом на его месте получают 1;

а_ij`= а<sub>ij</sub> - а<sub>tj</sub>`* а_ik = а_ij - а_tj * а_ik / а_tk ;

b_i`= b<sub>i</sub> - b<sub>t</sub>`* а_ik = b_i - b_t * а_ik / а_tk – из всех остальных строк вычитают преобразованную разрешающую строку, умноженную на элемент, стоящий в преобразуемой строке в разрешающем столбце (при этом на его месте получают 0, так как из него вычитают его же, умножив на 1);

D_j `= D<sub>j</sub> - а<sub>tj</sub>`* D_k =D_j - а_tj *D_k / а_tk ;

d`= d - b<sub>t</sub>`*D_k = d - b_t * D_k / а_tk – то же самое делают с критериальной строкой.

Докажем, что при применении этих формул мы действительно сможем построить новый план по тому же правилу (приравняв базисные переменные к свободным членам). Для этого нужно, чтобы новые свободные члены оказались неотрицательными, иначе такой план не будет допустимым.

Лемма 2 (о критерии допустимости таблицы). При преобразовании таблицы она сохраняет допустимость, т.е. b_i` ³ 0, "i.

Доказательство.

Свободные члены вычисляются по формулеb_i`= b_i - b_t * а_ik / а_tk.

Здесь b_i, b_t ³ 0 (т.к. предыдущая таблица – допустимая); а_tk > 0 (по способу выбора разрешающего элемента).

Если а_ik £ 0 , то b_i` ³ 0 (к неотрицательному числу прибавляют неотрицательное).

Если а_ik > 0, то  разделим обе части неравенства b_i - b_t * а_ik / а_tk ³ 0 на  а_ik . Получим: b_i - b_t * а_ik / а_tk ³ 0  Û b_i / а_ik - b_t / а_tk ³ 0 Û b_i / а_ik ³ b_t / а_tk

Последнее неравенство истинно по способу выбора разрешающего элемента. Следовательно, будет истинно и первое из этих трех неравенств, т.е. b_i` ³ 0.

Лемма доказана.

Таким образом, при правильном выборе разрешающего элемента преобразованной системе уравнений по-прежнему можно поставить в соответствие опорный план так же, как это делалось для исходной таблицы.

Лемма 3 (об изменении значения целевой функции). При переходе к следующему опорному плану значение целевой функции не убывает: d`³ d.

 Доказательство. Новое значение целевой функции вычисляется по формулеd`= d - b_t * D_k / а_tk. Здесь а_tk > 0, D_k < 0, b_t ³ 0.

Если b_t > 0, то d`> d.

Есди b_t = 0, то d`= d.

Лемма доказана.

Лемма 4 (о неограниченности целевой функции). Если в разрешающем столбце нет возможности выбрать разрешающий элемент (нет положительных элементов, все а_ik £ 0), то целевая функция задачи линейного программирования не ограничена.

Доказательство. Пусть D_k < 0, все а_ik £ 0.

Х^о = (b₁, . . .,b_m, 0, . . ., 0) - исходный опорный план; k-я переменная - небазисная.

Рассмотрим семейство планов:

Х^(a) = (b₁ - a_1ka, b₂ - a_2ka,. . .,b_m - a_mka, 0, . . ., 0, a, 0, . . .,0), a ³ 0.

Эти планы допустимые. В самом деле, так как все а_ik £ 0, все переменные здесь неотрицательные. В выполнении остальных ограничений легко убедиться, подставив эти планы в систему ограничений задачи (14). В самом деле, в каждом ограничении при этом будет получено:

b_i – a_ik*a + a_ik*a = b_i

Последнее ограничение будет иметь вид: z + 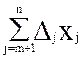= d. Подставим в него план Х^(a). При этом все слагаемые при небазисных переменных, кроме –го, обратятся в ноль (при небазисных тоже, потому что при этих переменных коэффициенты в критериальном ограничении равны нулю).

z + D_k*a = d; z = d - D_k*a. Так как D_k <0, a®+µ Þ z®+µ (при стремлении к бесконечности значение целевой функции тоже будет стремиться к плюс бесконечности). Таким образом, на допустимых планах целевая функция может принимать неограниченно большие значения.

Лемма доказана.

Теорема о сходимости симплекс-метода.Если после каждого этапа симплекс-метода значение целевой функции возрастает, то алгоритм дает решение задачи линейного программирования в конечное число шагов.