В таблице 9 критерий оптимальности нарушен в столбце коэффициентов при x2. Положительный коэффициент в этом столбце только один – 0,5. Это разрешающий элемент, в таблице 9 он выделен. Следовательно, x2 войдет в базис вместо x6. В результате преобразований будет получена таблица 10.
Для того, чтобы получить эту таблицу, диапазон ячеек А7:К11 скопируем на диапазон А12:К16. В В14 вместо x6 введем x2. Затем отредактируем диапазон D13:К16. Для этого в D14 введем формулу =E9/$F9. Она вводится для того, чтобы обе части второго (разрешающего) ограничения разделить на F9, т.е. на 0,5. В D13 введем формулу =D8-D$14*$F8. Скопируем последнюю формулу на диапазон ячеек D15:D16. Это делается для того, чтобы из всех остальных строк, вычесть преобразованную разрешающую, умноженную соответственно на -0,5, 0 и -1.
Выделим формулы в диапазоне D13:D16 и скопируем их на диапазон ячеек Е13:К16. В результате столбец коэффициентов при x2 станет единичным.
Тот же результат был бы получен, если бы в D16 вместо формулы =D11-D$14*$F11 стояла формула =СУММПРОИЗВ($C13:$C15;D13:D15)-D1, и именно она была бы скопирована на диапазон Е16:К16.
Таблица 10 – Оптимальная симплексная таблица
|
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
|
|
12 |
N |
xб |
cб |
B |
x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
x7 |
|
13 |
1 |
х3 |
2 |
5 |
-1 |
0 |
1 |
1 |
0 |
1 |
0 |
|
14 |
2 |
x2 |
0 |
8 |
3 |
1 |
0 |
2 |
-1 |
2 |
0 |
|
15 |
3 |
x7 |
0 |
7 |
-3 |
0 |
0 |
5 |
0 |
0 |
1 |
|
16 |
m+1 |
10 |
3 |
0 |
0 |
2 |
0 |
2 |
0 |
Таким образом, в таблице 10 записана система (17).
В критериальном ограничении последней симплексной таблицы нет отрицательных коэффициентов. Следовательно, оптимальный план найден. А именно, небазисные переменные x1 = x4= x5 = x6 = 0, а базисные (их список находится в столбце xб) равны свободным членам (в столбце В): x3 = 5, x2 = 8, x7 = 7. Оптимум равен 10.
Итак, Х(*) = Х(2) = (0; 8; 5; 0; 0; 0; 7), z(*) = z(2) = 10.
Алгоритм симплекс-метода можно представить в виде блок-схемы, приведенной на рисунке 26.
![]()
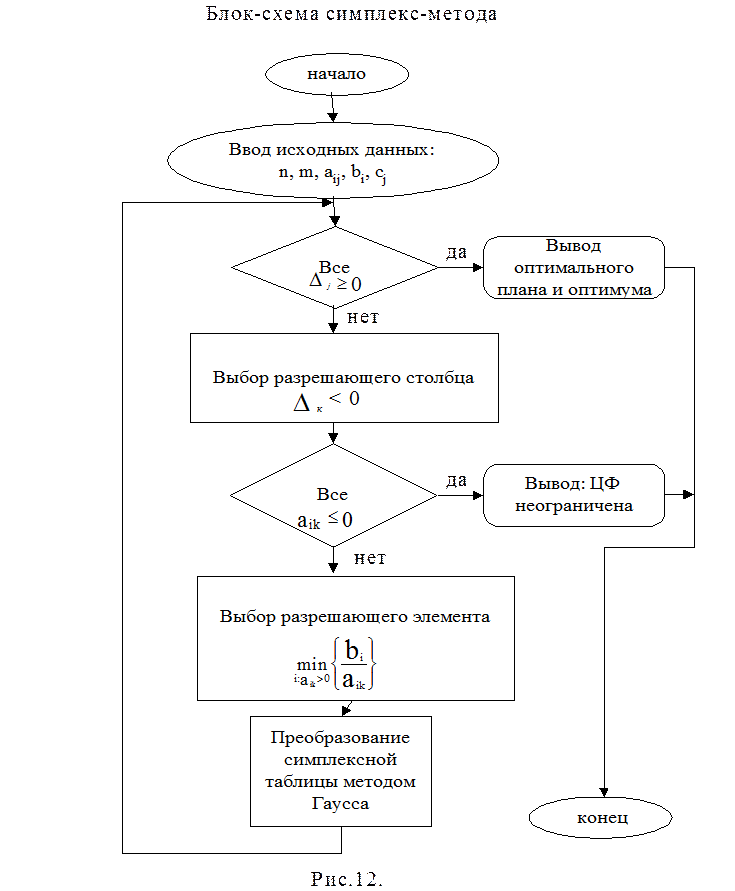
Рисунок 26 – Блок-схема симплекс-метода
Решение задачи на минимум отличается только критерием оптимальности - все коэффициенты критериального ограничения должны быть неположительны (соответственно, разрешающий столбец выбирается по положительному элементу).
При решении задач целесообразно соблюдать следующие рекомендации:
а) Если среди ограничений задачи линейного программирования имеются неравенства, или не все переменные являются неотрицательными, начните решение с приведения задачи к канонической форме. Проверьте, все ли свободные члены неотрицательны, и имеется ли базис. Если нет, проверьте, нельзя ли этого добиться простыми преобразованиями.
б) Чтобы избежать ошибки, разрешающий элемент в таблице следует выделять.
в) На каждой итерации симплекс-метода целесообразно проверять, соблюдены ли в таблице следующие элементарные правила:
1) Не должен нарушаться критерий допустимости. Отрицательный элемент в столбце В - признак ошибки в расчетах, причем скорее всего она была допущена при выборе разрешающей строки.
2) Должен присутствовать полный набор единичных столбцов при базисных переменных, причем единица должна стоять в той строке, которой эта переменная соответствует, а в остальных - нули.
3) Одно из средств контроля правильности вычислений - подсчет критериальной строки двумя способами: методом Гаусса и через сумму произведений (результаты должны совпадать).
4) При переходе к следующей симплексной таблице значение целевой функции должно, по крайней мере, не убывать (если задача на максимум) или не возрастать (если она на минимум).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.