Симплекс-метод решения задачи линейного программирования, страница 8

Доказательство. На каждом этапе мы получаем текущий опорный план (вершину ОДП). Число опорных планов конечно (не больше, чем число способов выбора m переменных из n - *). Так как по предположению целевая функция возрастает, то мы второй раз не получим пройденный план, а значит, в конечное число этапов получим решение.

Целевая функция не убывает по лемме 3. Если ее значение не изменяется, то возможно зацикливание (хотя оно встречается довольно редко). В систему может быть вставлен специальный блок для проверки на зацикливание. По той же лемме 3 значение целевой функции может не измениться только если b_t = 0, т.е. в очередном опорном плане базис был вырожденным.

Из формулы для пересчета целевой функции (d`= d - b_t * D_k / а_tk) следует, что при выборе разрешающего столбца можно заранее определить, на сколько изменится ее значение: на D_k * b_t / а_tk. Следовательно, если критерий оптимальности нарушен не в одном, а в нескольких столбцах таблицы, то выбрать в качестве разрешающего лучше тот из них, для которого это изменение будет больше. Тогда решение задачи может быть получено быстрее, за меньшее число этапов.

Вторая симплексная таблица для решенного примера примет вид таблицы 9.

Для того, чтобы получить ее в Microsoft Excel, следует скопировать диапазон ячеек А1:К6 на диапазон А7:К11. Затем отредактируем вспомогательную часть таблицы: в В8 вместо x₅ введем x₃, а в С8 вместо 0 введем 2.

Затем отредактируем диапазон D8:К11. Для этого в D8 введем формулу =D3/$G3*. Она вводится для того, чтобы обе части третьего ограничения разделить на G3, т.е. на 2.

В D9 введем формулу =D4-D$8*$G4. Скопируем последнюю формулу на диапазон ячеек  D10:D11. В результате в D10 появится формула =D5-D$8*$G5, а в D11 формула =D6-D$8*$G6. Это делается для того, чтобы из всех остальных строк, кроме разрешающей, вычесть преобразованную разрешающую (она в 8-й строке электронной таблицы), умноженную соответственно на 1 (в G4), 0 (в G5) и -2 (в G6).

Выделим формулы в диапазоне D8:D11 и скопируем их на диапазон ячеек Е8:К11. В результате столбец коэффициентов при x₃ станет единичным.

Таблица 9 – Вторая симплексная таблица

Таким образом, в таблице 9 записана система (16).

Отметим, что для пересчета критериального ограничения можно использовать два способа:

а) описанный выше метод Гаусса (поскольку это такое же линейное ограничение, как и остальные m ограничений);

б) можно заново перестроить его по выведенным ранее формулам D_j = 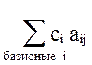- c_j; d = 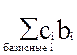 (по своей сути это означает выражение базисных переменных из ограничений через небазисные и подстановку их в критериальное ограничение).

При использовании для расчетов электронной таблицы способ (а) предпочтительнее.

Тем не менее, если ввести в D11 другую формулу =СУММПРОИЗВ($C8:$C10;D8:D10)-D1, и именно ее скопировать по строке до К11, то результат вычислений получится тем же самым, что приведен в таблице 9. В самом деле, d = 2*1 + 0*4 + 0*7 – 0 = 2 (здесь, в отличие от других столбцов, вычитать 0 не обязательно, но ячейка D1 все равно нулевая); D₁ = 2*(-2,5) + 0*1,5 + 0*(-3) – (-5) = 0; D₂ = 2*(-0,5) + 0*0,5 + 0*0 –
- 0 = -1;  коэффициент при базисной переменной D₃ == 2*1 + 0*0 + 0*0 – 2 = 0 и т.д.

Если в исходной симплексной таблице базисные переменные входят в целевую функцию, то в ней построить критериальную строку можно только способом (б).