Симплекс-метод решения задачи линейного программирования, страница 6

Идея дальнейшего решения заключается в том, чтобы в критериальном ограничении увеличивать первое слагаемое (z) за счет уменьшения суммы остальных (свободный член - постоянная величина). При этом в той сумме, которую необходимо уменьшить, отличные от нуля коэффициенты стоят только при небазисных переменных (так как базисным соответствуют единичные столбцы). Небазисные переменные равны нулю,  их значения можно только увеличивать. При этом увеличиваться должны значения тех небазисных переменных, при которых стоят отрицательные коэффициенты D_j (чтобы сумма уменьшалась)_. Однако увеличение этих переменных ограничивается другими уравнениями системы.

Лемма 1 (критерий оптимальности плана).Если все D_j ³ 0, то текущий опорный план - оптимальный.

Доказательство следует из того, что небазисные переменные равны нулю. Их можно только увеличивать, при этом, так как D_j ³ 0, то целевая функция уменьшается, так как в уравненим (z + 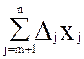 = d) значение d - const.

Рассмотрим исходную симплексную таблицу для решенного выше примера (таблица 8). Поскольку для расчетов предполагается использовать средства электронной таблицы Microsoft Excel, слева и сверху от таблицы 8 указаны номера строк и столбцов электронной таблицы.

В диапазон ячеек D1:К5 введены исходные данные примера. Исходя из них, заполнена вспомогательная часть таблицы в А2:С5. В D6 введена формула =-D1, которая затем скопирована по строке до К6 (таким образом введены свободный член и коэффициенты критериального ограничения).

Таблица 8 – Исходная симплексная таблица

Таким образом, в таблице 8 записана система (15).

Итак, если все D_j ³ 0, то задача решена (это критерий оптимальности для задачи на максимум). Если это не так, необходимо перейти к другому опорному плану. Для этого выберем столбец таблицы, в котором нарушен критерий оптимальности, т.е. некоторый k-й столбец, такой, что D_k < 0. Этот столбец называют разрешающим (очевидно, он не базисный, так как иначе было бы D_k = 0). Преобразуем симплексную таблицу таким образом, чтобы переменная х_к вошла в базис (т.е. в набор базисных переменных), а некоторая другая переменная из него вышла.

В этом примере среди коэффициентов D_j есть отрицательный: D₃  = -2 < 0 (k = 3). Поэтому при преобразовании системы (15) в систему (16) в базис входила переменная x₃. Далее в разделе 3.2.1 мы определяли, какую переменную следует вывести из базиса, и для этого подсчитывали отношения 2/2 и 5/1.

Для выбора переменной, которая должна выйти из базиса, для всех положительных элементов k-го столбца подсчитывают отношения b_i/a_iк и выбирают из них наименьшее. Соответствующую строку (пусть это будет
t-ая строка) также называют разрешающей, а коэффициент а_tk - разрешающим элементом.

В таблице 8 положительные a_iк = a_i3 находятся в первой и второй строках. Наименьшее из отношений b_i/a_iк соответствует первой строке: min {b₁/a₁₃; b₂/a₂₃ } = {2/2; 5/1} = {1; 5} = 1. Таким образом, разрешающая строка - первая, т.е. t = 1. Разрешающий элемент а_tk =  а₁₃ = 2. В таблице 8 он выделен заливкой. При преобразовании системы (15) в систему (16) из базиса выходила переменная x₅, которая соответствует первой строке.