Двойственность в линейном программировании

5 Двойственность в линейном программировании. 83

5.1 Понятие двойственности. 83

5.2 Экономическая интерпретация двойственной задачи. 87

5.3 Первая теорема двойственности. 88

5.4 Вторая теорема двойственности. 90

5.5 Третья теорема двойственности. 92

5.6 Пример решения сопряженных задач. 95

5.6.1 Задача, двойственная задаче о диете. 95

5.6.2 Выполнение основной теоремы двойственноти. 97

5.6.3 Выполнение теоремы о равновесии. 98

5.6.4 Выполнение теоремы об оценке. 99

5.7 Вопросы и упражнения. 105

5 Двойственность в линейном программировании

5.1 Понятие двойственности

Рассмотрим задачи линейного программирования в стандартной форме, записанные в матричной форме:

max CX

,

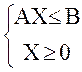где С = (с₁ . . . с_n), X = , B = , A =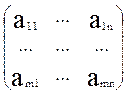  

min YB

,

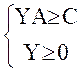где Y = (y₁ . . . y_m).

Здесь X, Y - переменные*; A, B, C - константы.

Задача (21) и любая эквивалентная ей задача линейного программирования называется двойственной задаче (20) и любой эквивалентной ей задаче.

Подчеркнем, что новых переменных вводится ровно столько, сколько в задаче (20) ограничений, т.е. m.

Поскольку любая задача линейного программирования может быть записана в стандартной форме, данное определение позволяет построить двойственную задачу для любой задачи линейного программирования.

Исходную задачу, по отношению к которой строится двойственная, иногда еще называют прямой задачей.

Теорема (о сопряженных задачах). Задача, двойственная двойственной, эквивалентна исходной.

Доказательство. Построим задачу линейного программирования, двойственную (21). Поскольку определение дает возможность построить двойственную задачу только для задачи в той же форме записи, что и задача (20), вначале преобразуем задачу (21) таким образом, чтобы форма ее записи была такой же.

Приведем задачу (21) к стандартной форме на максимум:

mах Y(-B)

 

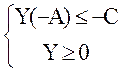
Транспонируем входящие сюда величины, чтобы порядок действий над векторами и матрицами был таким же, как и в задаче (20):

mах -B^ТY^Т

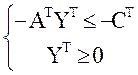
Теперь можно построить двойственную задачу в соответствии со сформулированным определением. Введем строку переменных Z.

min Z(-C^T)

 

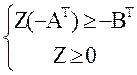
Эта задача является двойственной к двойственной. Преобразуем ее.

mах СZ^Т

 

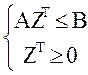
Эта задача эквивалентна задаче (20) с точностью до обозначения.

Теорема доказана.

Таким образом, двойственность является взаимной. Пара взаимно двойственных задач называется парой сопряженных задач.

Рассмотрим задачу в канонической форме. Чтобы построить задачу, двойственную к ней, преобразуем ее к стандартной форме.

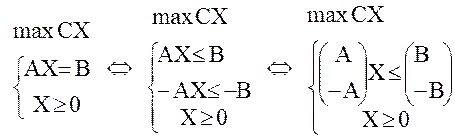
Построим теперь двойственную задачу. Отметим, что число ограничений задачи возросло в два раза (каждое уравнение преобразовано в два неравенства). Вектор-строку переменных двойственной задачи разобьем на две части, в каждую из которых будет входить равное число переменных, и обозначим его (U,V) = (u₁, …, u_m, v₁, …, v_m).

При этом во всех линейных выражениях компоненты вектора В и матрицы А можно вынести за скобки, а в скобках останется разность векторов U = (u₁, …, u_m) и V = (v₁, …, v_m). Например, при перемножении строки переменных на первый столбец матрицы А будет получено:
(a₁₁u₁ + a₂₁u₂ + … + a_m1u_m - a₁₁v₁ - a₂₁v₂ - … - a_m1v_m = a₁₁(u₁ - v₁) + a₂₁(u₂ – v₂) + … + a_m1(u_m – v_m); - и т.д.

 

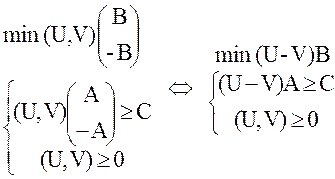
Обозначим U - V = Y. При этом переменные Y = (u₁ - v₁; …; u_m – v_m) =
= (y₁ . . . y_m) не ограничены по знаку. Тогда двойственная задача примет вид:

min YB

YA ³ C

Итак, ограничениям-уравнениям поставлены в соответствие неограниченные по знаку переменные. Поскольку двойственность взаимна, можно сказать, что и неограниченным по знаку переменным следует ставить в соответствие ограничения уравнения, а не неравенства.

На основании проведенных рассуждений можно сделать вывод, что для построения двойственной задачи не обязательно каждый раз приводить задачу линейного программирования к стандартной форме, а именно нет необходимости преобразовывать уравнения к неравенствам, а не ограниченные по знаку переменные - к неотрицательным. Пусть в задаче в смешанной форме первые m` ограничений – уравнения, а остальные m-m` - неравенства; и первые n` переменных неотрицательны, а остальные n-n` переменных по знаку могут быть любыми. Между задачей линейного программирования в смешанной форме и двойственной ей задачей линейного программирования можно установить следующее соответствие:

max cjxj	min biyi
aijxj = bi,	(22)   aijyi ³ cj,
aijxj £ bi,	aijyi = cj,
xj ³ 0,	yi ³ 0,
xj  0,	yi  0,

Сформулируем ряд правил построения двойственной задачи:

а) Переменные двойственной задачи соответствуют ограничениям исходной задачи, а ограничения - переменным.

б) Если исходная задача линейного программирования задана на максимум, то двойственная строится на минимум, и наоборот.

в) В задаче линейного программирования на максимум в ограничениях-неравенствах должен стоять знак £, а на минимум - ³.

г) Ограничениям-неравенствам исходной задачи соответствуют неотрицательные двойственные переменные, а уравнениям – не ограниченные по знаку переменные.