Двойственность в линейном программировании, страница 4

y_i^*(a_ijx_j^* - b_i) = 0,

Т.е. допустимые планы сопряженных задач являются оптимальными тогда и только тогда, когда произведение основной переменной одной задачи на дополнительную переменную в соответствующем ограничении другой задачи равно нулю для всех переменных и ограничений.

Следствие.

Для Х^*ÎОДП(I), Y^*Î ОДП(II)

Х^*, Y^*- оптимальные

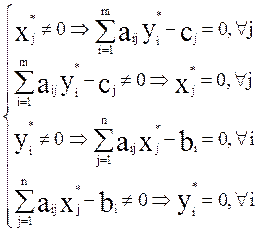
Т.е. в решении сопряженных задач если ограничение не связанное (выполняется как строгое неравенство, дополнительная переменная отлична от нуля), то соответствующая переменная двойственной задачи равна нулю. Если переменная отлична от нуля, то соответствующее ограничение двойственной задачи является связанным (выполняется, как равенство).

На примере задачи производственного планирования можно дать экономическую интерпретацию второй теоремы двойственности. Она позволяет рассматривать переменные двойственной задачи как оценки дефицитности соответствующих ресурсов.

Дополнительные переменные исходной задачи представляют собой остатки каждого вида ресурса. Если ресурс расходуется полностью (дополнительная переменная равна нулю), ресурс дефицитен. Если ресурс остается (дополнительная переменная положительна), то он дефицитным не является.

Выражени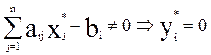е () означает, что если некоторый ресурс не является дефицитным (имеется в избытке), то оценка его дефицитности y_i равняется нулю. Например, для задачи, решенной в разделе 3.3, второй ресурс - патока - не был израсходован полностью, т.е.
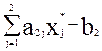 = 0,2х₁^* + 0,4х₂^* – 600 = -х₄^* = -77,333 ¹ 0. Поэтому оценка дефицитности патоки у₂^* = 0 (иначе не выполнялась бы теорема о равновесии, согласно которой должно быть х₄^**у₂^* = 0).

Выражение (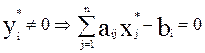) означает, что если оценка дефицитности отлична от нуля, то ресурс расходуется полностью, его остаток равен нулю. Например, зная, что  у₁^* = 125,33 ¹ 0, можно утверждать, что х₃^* = 0, т.е. сахарный песок израсходован полностью (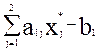 = 0,8х₁^* +
+ 0,5х₂^* – 800 = 0). Зная, что  у₃^* = 773,33 ¹ 0, можно утверждать, что х₅^* = 0, т.е. фруктовое пюре израсходовано полностью (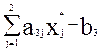 = 0,01х₁^* + 0,1х₂^*–
- 120 = 0). Таким образом, выполняются требования теоремы о равновесии х₃^**у₁^* = 0 и х₅^**у₃^* = 0.

Выражение (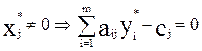) означает, что если принято решение производить некоторый вид продукции, т.е. x_j > 0, то ограничения двойственной задачи выполняются, как равенства. Поскольку в рассматриваемом примере оба вида карамели производятся (х₁^* = 266,67 ¹ 0; х₂^* = 1173,3 ¹ 0), обе дополнительные переменные двойственной задачи должны равняться нулю: у₄^* = у₅^* = 0 (0,8у₁ + 0,2у₂ + 0,01у₃ – 108 = у₄; 0,5у₁ + 0,4у₂ + 0,1у₃ –140 = у₅). Таким образом, выполняются требования теоремы о равновесии х₁^**у₄^* = 0 и х₂^**у₅^* = 0.

Выражение (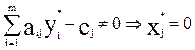) означает, что если бы ограничение двойственной задачи выполнялось, как строгое неравенство, то производить соответствующую продукцию было бы невыгодно, x_j = 0. В рассматриваемом примере этот случай не встречается, т.к. выгодно производить и ту, и другую карамель. Предположим, что при других величинах прибыли на тонну карамели выпускать одну из них, например, «Снежинку», стало невыгодно, и х₁^*= 0. Тогда переменная у₄^* могла бы быть отличной от нуля, положительной. Но это не обязательно имело бы место.

Отметим, что во всех четырех выражениях знак следствия направлен только в одну сторону. В самом деле, чтобы произведение равнялось нулю, хотя бы один из сомножителей должен быть нулевым, но могут равняться нулю и оба. Поэтому из того, что один из них – ненулевой, следует, что другой обязательно равен нулю. А вот из того, что один из сомножителей равен нулю, вовсе не следует, что другой должен быть ненулевым: он может быть ненулевым, а может быть также равен нулю.

5.5 Третья теорема двойственности