Двойственность в линейном программировании, страница 2

д) Неотрицательным переменным исходной задачи соответствуют ограничения неравенства двойственной задачи, а не ограниченным по знаку - уравнения.

Если обе сопряженные задачи записаны в стандартной форме, их называют симметричными сопряженными задачами.

Например, построим задачу, двойственную к следующей задаче:

min 2х₁ + 3х₂ - 4х₃ + х₅

4х₁ - 3х₂ - х₃ + х₄ + х₅ £10

х₁ + 4х₂ + х₃ + х₅ = 15

2х₁ - 4х₂ - х₃ + х₄ ³ 3

х_{1-3, 5} ³ 0

Так как задача на минимум, умножим обе части первого ограничения на -1, чтобы получить знак неравенства ³: -4х₁ + 3х₂ + х₃ - х₄ - х₅ ³ -10.

Так как в прямой задаче три ограничения на пять переменных, двойственная задача будет включать пять ограничений на три переменных.

Целевая функция двойственной задачи максимизируется, так как прямая задача поставлена на минимум. Коэффициенты целевой функции двойственной задачи представляют собой свободные члены прямой задачи.

Первое ограничение двойственной задачи соответствует переменной х₁ прямой задачи, поэтому коэффициенты этого ограничения берут из столбца коэффициентов при х₁, а свободный член – из целевой функции прямой задачи. Так как х₁ ³ 0, это ограничение – неравенство. Так как двойственная задача на максимум, знак неравенства £. Аналогично строятся второе, третье и пятое ограничения. Четвертое ограничение соответствует переменной х₄, знак которой может быть любым. Поэтому оно – уравнение.

Переменные y₁ и y₃ соответствуют первому и третьему ограничениям прямой задачи, которые представляют собой неравенства. Поэтому эти переменные – неотрицательные. Второе ограничение прямой задачи – уравнение, поэтому переменная y₂ не ограничена по знаку.

max -10y₁ + 15y₂ + 3y₃

-4y₁ + y₂ + 2y₃ £ 2

3y₁ + 4y₂ - 4y₃ £ 3

y₁ + y₂ - y₃ £ -4

-y₁ + y₃ = 0

-y₁ + y₂ £ 1

y_1,3 ³ 0

5.2 Экономическая интерпретация двойственной задачи

Рассмотрим интерпретацию двойственной задачи на примере задачи производственного планирования (предприятие может выпускать n видов продукции из m видов ресурсов, требуется установить объемы выпуска каждого вида, при которых общая выручка была бы максимальной):

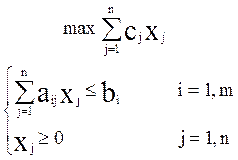
где с_j - цена реализации j-го вида продукции,

а_ij - затраты i-го ресурса на единицу j-го вида продукции,

b_i - запас i-го ресурса,

x_j - выпуск j-го вида продукции (переменные).

Рассмотрим эту же ситуацию с точки зрения ограничений. Предположим, что вместо того, чтобы выпускать продукцию, предприятие собирается продать предназначенные для ее производства ресурсы. Другое предприятие может купить у «исходного» эти ресурсы по некоторым ценам y_i, которые и будут представлять собой переменные двойственной задачи:

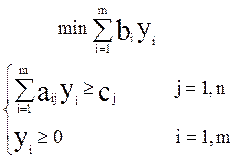
Вид целевой функции двойственной задачи объясняется тем, что предполагаемый покупатель стремится минимизировать свои затраты.

Рассмотрим левые части ограничений. Они представляют собой суммы произведений затрат каждого вида ресурса (на единицу выпуска данного вида продукции) на цены этих ресурсов. Что такое 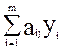? Именно такую сумму выручит «исходное» предприятие, если продаст ресурсы, предназначенные для выпуска единицы j–го вида продукции. И оно предприятие продаст свои ресурсы только в том случае, если это будет для него не менее выгодно, чем производить продукт, т.е. эта сумма будет не меньше, чем цена за единицу произведенного продукта каждого вида с_j. Этим объясняется знак в ограничениях двойственной задачи.

Построим задачу, двойственную к задаче, поставленной в разделе 1.1. Для этого введем три двойственных переменных: у₁ – двойственная оценка сахарного песка, у₂ - патоки, у₃ - фруктового пюре. Двойственная задача примет вид:

max 800у₁ + 600у₂ + 120у₃

0,8у₁ + 0,2у₂ + 0,01у₃ ³ 108

0,5у₁ + 0,4у₂ + 0,1у₃ ³ 140

у_1-3 ³ 0

Целевую функцию этой задачи (800у₁ + 600у₂ + 120у₃) можно рассматривать, как затраты покупателя на приобретение 800 т сахарного песка, 600 т патоки и 120 т фруктового пюре.